WORKSHEET ON SIMILAR TRIANGLES

Problem 1 :

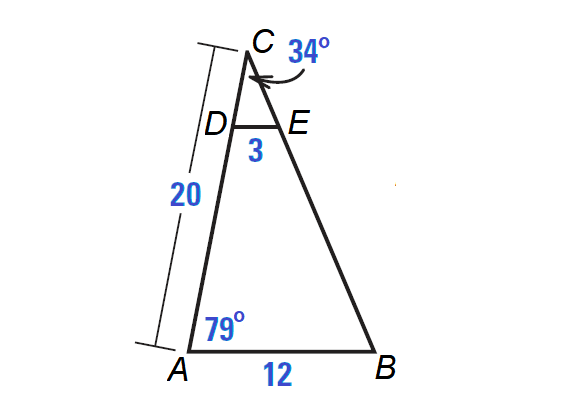
In the diagram shown below ΔACB ∼ ΔDCE.

a. Write the statement of proportionality.

b. Find ∠CDE.

c. Find DC and AD. 

Problem 2 :

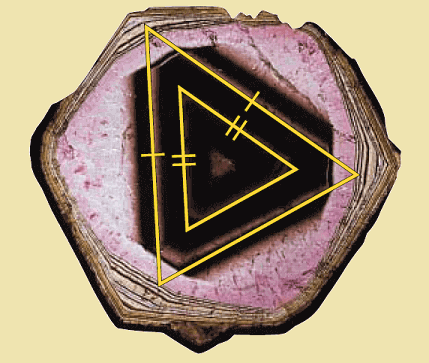
Color variations in the tourmaline crystal shown below lie along the sides of isosceles triangles. In the triangles each vertex angle measures 52°. Explain why the triangles are similar.

Problem 3 :

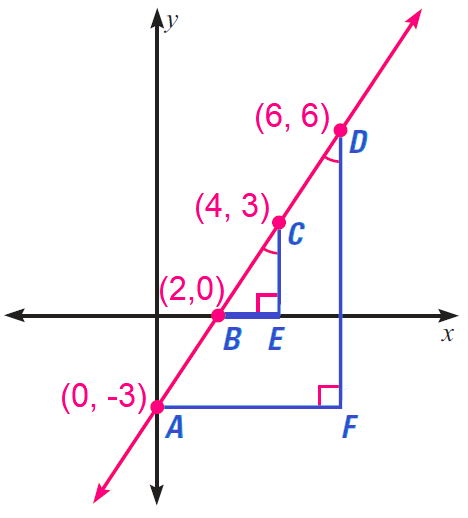
Use properties of similar triangles to explain why any two points on a line can be used to calculate the slope. Find the slope of the line using both pairs of points shown.

Problem 4 :

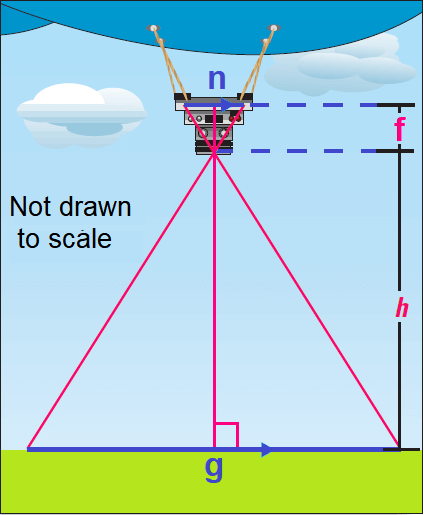
Low-level aerial photos can be taken using a remote-controlled camera suspended from a blimp. we want to take an aerial photo that covers a ground distance g of 50 meters. Use the proportion f/h  =  n/g to estimate the altitude h that the blimp should fly at to take the photo. In the proportion, use f = 8 cm and n = 3 cm. These two variables are determined by the type of camera used. 

Problem 5 :

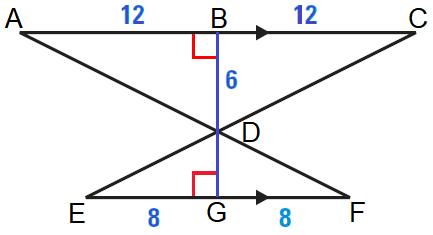
Find the length of the altitude DG in the diagram shown below. 

Answers

1. Answer :

Part (a) :

DC / AC  =  CE / CB  =  ED / BA

Part (b) :

Because ΔACB ∼ ΔDCE,

∠A  ≅  ∠CDE

Then, we have

∠CDE  =  ∠A  =  79°

Part (c) :

Write proportion. 

ED / BA  =  DC / AC

Substitute. 

3 / 12  =  DC / 20

Multiply each side by 20. 

20 ⋅ (3 / 12)  =  (DC / 20) ⋅ 20

Simplify. 

5  =  DC

Because AD  =  AC - DC, 

AD  =  20 - 5

AD  =  15

So, DC is 5 units and AD is 15 units. 

2. Answer :

Because the triangles are isosceles, we can determine that each base angle is 64°. Using the AA Similarity Postulate, we can conclude that the triangles are similar.

3. Answer :

By the AA Similarity Postulate ΔBEC ∼ ΔAFD, so the ratios of corresponding sides are the same.

In particular,

CE/DF  =  BE/AF

By a property of proportions, we have

CE/BE  =  DF/AF

The slope of a line is the ratio of the change in y to the corresponding change in x. The ratios CE/BE and DF/AF represent the slopes of BC and AD respectively. 

Because the two slopes are equal, any two points on a line can be used to calculate its slope. We can verify this with specific values from the diagram.

Using slope formula,

Slope of BC  =  (3 - 0)/(4 - 2)  =  3/2

Slope of AD  =  [6 - (-3)]/(4 - 2)  =  9/6  =  3/2

4. Answer :

Write proportion. 

f/h  =  n/g

Substitute.

8/h  =  3/50

By reciprocal property of proportion, 

h/8  =  50/3

Multiply each side by 8. 

8 ⋅ (h/8)  =  8 ⋅ (50/3)

Simplify. 

h  ≈  133

So, the blimp should fly at an altitude of about 133 meters to take a photo that covers a ground distance of 50 meters.

5. Answer :

Find the scale factor of ΔADC to ΔFDE. 

AC/FE  =  (12 + 12)/(8 + 8)

AC/FE  =  24/16

AC/FE  =  3/2

Now, because the ratio of the lengths of the altitudes is equal to the scale factor, we can write the following equation.

DB/DG  =  3/2

Substitute 6 for DB and and solve for DG.

6/DG  =  3/2

By reciprocal property of proportion, 

DG/6  =  2/3

Multiply each side by 6. 

6 ⋅ (DG/6)  =  (2/3) ⋅ 6

Simplify. 

DG  =  4

So, the length of the altitude DG is 4 units. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.