WORKSHEET ON WORD PROBLEMS ON LINEAR EQUATION IN ONE VARIABLE

Problem 1 : 

Sum of two numbers is 95. If one exceeds the other by 15, find the numbers.

Problem 2 :

A book has 50 more pages than nother book. If the total number of pages in both books is 400, how many pages does the larger book have?

Problem 3 :

If 15 is added to one-fourth of a number, the result is 4 times the number. What is the number? 

Problem 4 :

If m + 6 is divided by 2 is 4 less than 4m, what is the value of m?

Problem 5 :

A hair shampoo comes in regular bottles and deluxe bottles. A deluxe bottle contains 6 more ounces of shampoo than a regular once. If four regular bottles and three deluxe bottles contain a total of 74 ounces of shampoo, how many ounces shampoo does a deluxe bottle contain?

Problem 6 :

Travelling a an average speed of 40 miles per hour, a bus takes 3 hours to complete its morning route. At what average speed, in miles per hour, must the bus travel if it is to complete its morning route in 2.5 hours? 

Problem 7 :

Two numbers are in the ratio 5 : 3. If they differ by 18, what are the numbers ?

Problem 8 : 

If you subtract ½ from a number and multiply the result by ½, you get ⅛. What is the number?

Problem 9 :

The perimeter of a rectangular swimming pool is 154 m. Its length is 2 m more than twice its width. What are the length and the width of the pool ?

Problem 10 :

The base of an isosceles triangle is ⁴⁄₃ cm. The perimeter of the triangle is 4²⁄₁₅ cm. What is the length of either of the remaining equal sides?

Answers

1. Answer :

Let x be one of the two numbers.

Then, the other number is (x + 15).

Given : Sum of two numbers is 95.

x + (x + 15) = 95

Simplify.

x + x + 15 = 95

2x + 15 = 95

Subtract 15 from each side.

2x = 80

Divider each side by 2.

x = 40

x + 15 = 40 + 15 = 55

The two numbers are 40 and 55.

2. Answer :

Let x be the number of pages in the smaller book.

Then, the number of pages in the larger book is (x + 50).

Given : Total number of pages in both books is 400.

x + (x + 50) = 400

x + x + 50 = 400

2x + 50 = 400

Subtract 50 from both sides.

2x = 350

Divide both sides by 2.

x = 175

x + 50 = 175 + 50 = 225

The larger book has 225 pages.

3. Answer :

Let x be the number.

Given : 15 is added to one-fourth of the number results times the number.

(¼)x + 15 = 4x

ˣ⁄₄ + 15 = 4x

Multiply both sides by 4.

4(ˣ⁄₄ + 15) = 4(4x)

4(ˣ⁄₄) + 4(15) = 16x

x + 60 = 16x

Subtract x from both sides.

60 = 15x

Divide both sides by 15.

4 = x

The number is 4.

4. Answer :

(m + 6) ÷ 2 = 4m - 4

⁽ᵐ ⁺ ⁶⁾⁄₂ = 4m - 4

Multiply both sides by 2.

2[⁽ᵐ ⁺ ⁶⁾⁄₂] = 2(4m - 4)

m + 6 = 8m - 8

Subtract m from both sides.

6 = 7m - 8

Add 8 to both sides.

14 = 7m

Divide both sides by 7.

2 = m

5. Answer :

Let the regular bottle contain x ounces shampoo.

Then, the deluxe bottle contains (x + 6) ounces.

Given : Four regular bottles and three delux bottles contain a total of 74 ounces of shampoo.

4x + 3(x + 6) = 74

4x + 3x + 18 = 74

7x + 18 = 74

Subtract 18 from both sides.

7x = 56

Divide both sides by 7.

x = 8

x + 6 = 8 + 6 = 14

A deluxe bottle contains 14 ounces shampoo.

6. Answer :

We know the following relaatiobship between speed, time and distance.

speed ⋅ time = distance ----(1)

Using the above relationship to find the morning route distance.

Substitute, speed = 40 and time = 3 in (1).

40 ⋅ 3 = Distance

120 = Distance

Morning route distance = 120 miles

Let x be the average speed to cover the morning distance 120 miles in 2.5 hours.

Substitute, speed = x, time = 2.5 and distance = 120 in (1) and solve for x.

x ⋅ 2.5 = 120

2.5x = 120

Divide both sides by 120.

x = 48

The bust must travel at an average speed of 48 miles per hour to complete its morning route in 2.5 hours.

7. Answer :

From the ratio 5 : 3, the two numbers can be assumed as

5x and 3x

Given : The two numbers differ by 18.

So, we have

5x - 3x  =  18

2x  =  18

Divide each side by 2. 

2x/2  =  18/2

x  =  9

5x  =  5(9)  =  45

3x  =  3(9)  =  27

Hence, the two numbers are 45 and 27.

8. Answer :

Let x be the required number. 

From, the given information, we have 

(x - ½) ⋅ ½  = ⅛

Multiply each side by 2. 

(x - ½) ⋅ ½ ⋅ 2 = ⅛ ⋅ 2

(x - ½) ⋅ 1 = ¼

x - ½ = ¼

Add ½ to each side. 

x = ¼ + ½

x = ¼ + ²⁄₄

x = ⁽¹ ⁺ ²⁾⁄₄

x = ¾

The required number is ¾.

9. Answer :

Let l be the length and w be the width of the swimming pool.  

Given : Length is 2 m more than twice its width. 

Then, the length is 

l = 2w + 2

Given : The perimeter of the swimming pool is 154 m. 

2l + 2w = 154

Substitute l = 2w + 2.

2(2w + 2) + 2w = 154

Simplify.

4w + 4 + 2w = 154

6w + 4 = 154

Subtract 4 from each side.

6w = 150

Divide each side by 6.

w = 25

Then, the length is 

l = 2(25) + 2

l = 50 + 2

l = 52

The length and width of the rectangular swimming pool are 52 m and 25 m respectively. 

10. Answer :

Let x be the length of each of the remaining two equal sides. 

So, the sides of the triangle are

x, x and ⁴⁄₃

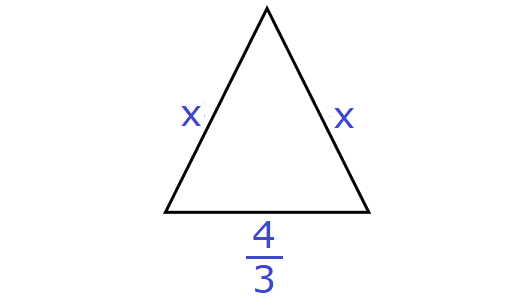
Given : The perimeter of the triangle is 4²⁄₁₅ cm cm.

x + x + ⁴⁄₃ = 4²⁄₁₅

2x + ⁴⁄₃ = ⁶²⁄₁₅ 

Subtract ⁴⁄₃ from each side.  

2x = ⁶²⁄₁₅ - ⁴⁄₃

2x = ⁽⁶² ⁻ ²⁰⁾⁄₁₅

2x = ⁴²⁄₁₅

2x = ¹⁴⁄₅

Divide each side by 2.

2x = (¹⁴⁄₅) ÷ 2

x = (¹⁴⁄₅) x (½)

x = ⁷⁄₅

x = 1⅖

Length of either of the remaining equal sides is 1⅖ cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.