WRITE A POLYNOMIAL FROM ITS ROOTS

Root is nothing but the value of the variable that we find in the equation.To get a equation from its roots, first we have to convert the roots as factors. By multiplying those factors we will get the required polynomial.

For example,

2 and 3 are the roots of the polynomial then we have to write them as

x  =  2 and x  =  3

To convert these as factors, we have to write them as

(x - 2) and (x - 3)

The product of those factors will give the polynomial. Because we have two factors, we will get a quadratic polynomial.

Number of factors  =  Highest exponent of the polynomial

Note :

Roots and zeroes are same.

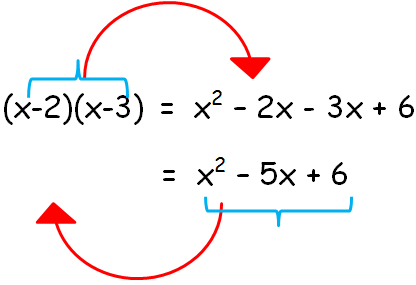
Example 1 :

Write the polynomial function of the least degree with integral coefficients that has the given roots.

0, -4 and 5

Solution :

Step 1 :

0, -4 and 5 are the values of x.

So we can write these values as

x  =  0, x  =  -4 and x  =  5

Step 2 :

Now convert the values as factors.

(x - 0), (x + 4), (x - 5) are the factors of the required polynomial.

Step 3 :

Number of factors  =  3 

Then, we will get a cubic polynomial. 

By multiplying the above factors we will get the required cubic polynomial.

So, the required polynomial is 

=  (x - 0)(x + 4)(x - 5)

=  (x-0)(x² - 5x + 4x - 20)

=  x(x² - x - 20)

=  x³ - x² - 20x

Example 2 :

Write the polynomial function of the least degree with integral coefficients that has the given roots.

3, 4/5 and 5/2

Solution :

Step 1 :

3, 4/5 and 5/2 are the values of x. So we can write these values as

x  =  3, x  =  4/5 and x  =  5/2

Step 2 :

Now convert the values as factors.

(x - 3), (x - 4/5) and (x - 5/2) are the factors of the required polynomial.

Step 3 :

Number of factors  =  3

Then, we will get a cubic polynomial.

By multiplying the above factors we will get the required cubic polynomial.

So, the required polynomial is 

=  (x - 3)(x - 4/5)(x - 5/2)

=  (x - 3)(x² - 5x/2 - 4x/5 + 2)

=  (x - 3)(x² - 33x/10 + 2)

=  (x - 3)(x² - 33x/10 + 2)

=  x³ - 33x²/10 + 2x - 3x² + 99x/10 - 6

Combine the like terms. 

=  x³ - 63x²/10 + 119x/10 - 6

Example 3 :

Write the polynomial function of the least degree with integral coefficients that has the given roots.

-5, 0 and 2i

Solution :

Step 1 :

-5, 0 and 2i are the values of x.

Because 2i is the complex number, its conjugate must also be another root. 

So, the required polynomial is having four roots.

Step 2 :

Now convert the values as factors.

(x + 5), (x - 0), (x - 2i) and (x + 2i) are the factors of the required polynomial.

Step 3 :

Number of factors = 4

Then, we will get a polynomial of degree 4.

By multiplying the above factors we will get the required polynomial.

So, the required polynomial is 

=  (x + 5)(x - 0)(x - 2i)(x + 2i)

=  x(x + 5)(x - 2i)(x + 2i)

=  (x² + 5x)[x² - (2i)²]

=  (x² + 5x)(x² - 4i²)

=  (x² + 5x)[(x² - 4(-1)]

=  (x² + 5x)[(x² - 4(-1)]

=  (x² + 5x)(x² + 4)

=  x⁴ + 4x² + 5x³ + 20x

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.