WRITE DOWN THE FACTORS OF THE GIVEN NUMBERS

Factor :

A factor is a number that divides into another number exactly and without leaving a remainder.

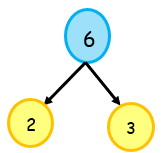
Here 2 and 3 are factors. 6 is divisible by both 2 & 3.

Example 1 :

List all the factors of 9.

Solution :

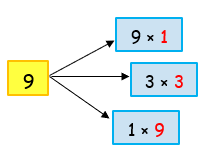
So, the factors of 9 are 1, 3, 9.

Example 2 :

List all the factors of 12

Solution :

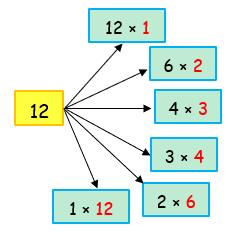
So, the factors of 12 are 1, 2, 3, 4, 6, 12.

Example 3 :

List all the factors of each of the following numbers :

1) 10

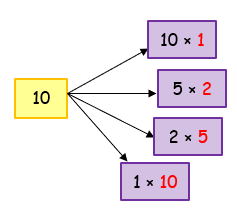So, the factors of 10 are 1, 2, 5, 10

2) 18

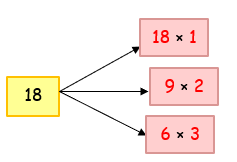So, the factors of 18 are 1, 2, 3, 6, 9, 18.

3) 30

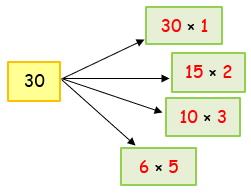So, the factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30

4) 35

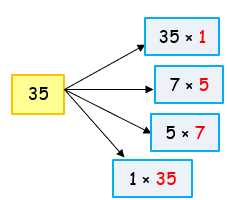So, the factors of 35 are 1, 5, 7, 35.

5) 44

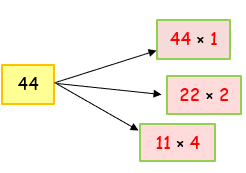So, the factors of 44 are 1, 2, 4, 11, 22, 44.

6) 56

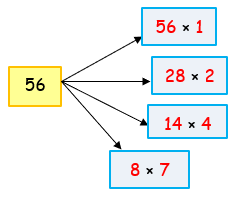So, the factors of 56 are 1, 2, 4, 7, 8, 14, 28, 56

7) 50

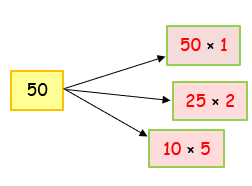So, the factors of 50 are 1, 2, 5, 10, 25, 50.

8) 84

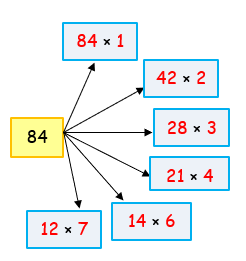So, the factors of 84 are 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84

Example 4 :

Complete the factorization given below :

Solution :

Example 5 :

Write the largest factor of each of the following numbers

(a)  12

Solution :

By writing the divisors of 12, we get.

1, 2, 3, 4, 6, 12

Excluding itself 6 is greater. So, 6 is the largest factor of 12.

(b)  18

Solution :

By writing the divisors of 18, we get.

1, 2, 3, 6, 9, 18

Excluding itself 9 is greater. So, 9 is the largest factor of 18.

(c)  27

Solution :

By writing the divisors of 27, we get.

1, 3, 9, 27

Excluding itself 9 is greater. So, 9 is the largest factor of 27.

(d)  48

Solution :

By writing the divisors of 48, we get.

1, 2, 3, 4, 6, 8, 12, 16, 48

Excluding itself 16 is greater. So, 16 is the largest factor of 48.

(d)  44

Solution :

By writing the divisors of 44, we get.

1, 2, 4, 11, 22, 44

Excluding itself 22 is greater. So, 22 is the largest factor of 44.

(e)  75

Solution :

By writing the divisors of 75, we get.

1, 3, 5, 15, 25, 75

Excluding itself 25 is greater. So, 25 is the largest factor of 75.

(f)  90

Solution :

By writing the divisors of 90, we get.

1, 3, 5, 9, 10, 15, 30, 45, 90

Excluding itself 45 is greater. So, 45 is the largest factor of 90.

(g)  39

Solution :

By writing the divisors of 39, we get.

1, 3, 13, 39

Excluding itself 13 is greater. So, 13 is the largest factor of 39.

Example 6 :

Which of the following is the factor of 72?

i) 8 and 9    ii) 12 and 7     iii) 36 and 36

Solution :

72 can be broken into product of two terms in many ways.

72 = 36 x 2

72 = 3 x 24

72 = 8 x 9

So, option (i) is correct.

Example 7 :

Product of first three prime number is

i) 20   ii) 30    iii) 40     iv) 6

Solution :

Prime numbers are 2, 3, 5, 7, 11, .........

First three prime numbers = 2, 3 and 5

= 2 x 3 x 5

= 30

So, option (ii) is correct.

Example 8 :

H.C.F of two prime number is__________. 

Solution :

Let us consider two prime numbers.

Consecutive prime numbers are

2 and 3

Two prime numbers which are not consecutive

13 and 23

The highest common factor of these two prime numbers is 1.

Example 9 :

Rahul has 18 oranges, 27 pears and 12 bananas. He wants to make fruit basket with an equal amount of each fruit in each basket. What is the largest number of fruit basket he can made?

Solution :

Number of oranges = 18

Number of pears = 27

Number of bananas = 12

Finding the greatest common factor of these three numbers, we get to know that how many fruits should be chosen from each category.

18/3 ==> 6 baskets of oranges

27/3 ==> 9 baskets of pears

12/3 ==> 4 baskets of bananas

Total number of baskets = 6 + 9 + 4

= 19 baskets.

Example 10 :

Find the common factors in each case:

(a) 10, 15

Factors of 10 : 

Factors of 15 :

Common factors of 10 and 15 :

Solution :

• Factors of 10 : 1, 2, 5, 10
• Factors of 15 : 1, 3, 5, 15

Common factors of 10 and 15 is 5

Example 11 :

5, 10, 25

Factors of 5 :

Factors of 10 :

Factors of 25 :

Common factors of 5, 10 and 25 :

Solution :

• Factors of 5 : 1 and 5
• Factors of 10 : 1, 2, 5 and 10
• Factors of 25 : 1, 5, 25

The highest common factor is 5.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.