WRITE EQUATIONS FOR PROPORTIONAL RELATIONSHIPS FROM TABLES

Example 1 :

Determine the constant of proportionality for each table and also write an equation for the relationship between x and y.

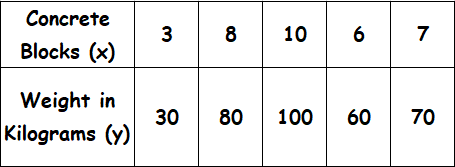
Solution :

To find the constant of proportionality, we have to divide y by x.

Ratio of y to x :

30/3 = 10

80/8 = 10

100/10 = 10

60/6 = 10

70/7 = 10

The ratio for each pair of x- and y-values is 10. So, the variables have a proportional relationship.

So, every concrete block weighs 10 kilograms. A proportional relationship between x and y can be modeled by the equation y = kx.

Here the value of k is 10.

So, the required equation for the relationship between x and y is y = 10x.

Example 2 :

Determine the constant of proportionality for each table.

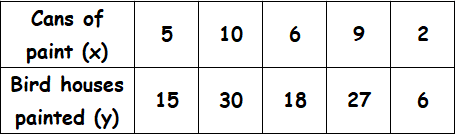
Solution :

To find the constant of proportionality, we have to divide y by x.

Ratio of y to x :

15/5 = 3

30/10 = 3

18/6 = 3

27/9 = 3

6/2 = 3

The ratio for each pair of x- and y-values is 3. So, the variables have a proportional relationship.

So, every can of paint you could paint 3 bird houses.

A proportional relationship between x and y can be modeled by the equation y = kx.

Here the value of k is 3.

So, the required equation for the relationship between  x and y is y = 3x.

Example 3 :

Determine the constant of proportionality for each table.

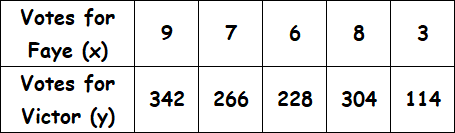
Solution :

To find the constant of proportionality, we have to divide y by x.

Ratio of y to x :

342/9 = 38

266/7 = 38

228/6 = 38

304/8 = 38

114/3 = 38

The ratio for each pair of x- and y-values is 38. So, the variables have a proportional relationship.

So, every vote for Faye there were 38 votes for Victor.

A proportional relationship between x and y can be modeled by the equation y = kx.

Here the value of k is 38.

So, the required equation for the relationship between x and y is y = 38x.

Example 4 :

Determine the constant of proportionality for each table.

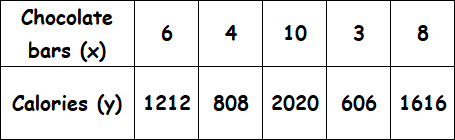
Solution :

To find the constant of proportionality, we have to divide y by x.

Ratio of y to x :

1212/6 = 202

808/4 = 202

2020/10 = 202

606/3 = 202

1616/8 = 202

The ratio for each pair of x- and y-values is 202. So, the variables have a proportional relationship.

So,every chocolate bar has 202 calories. 

A proportional relationship between x and y can be modeled by the equation y = kx.

Here the value of k is 202.

So, the required equation for the relationship between  x and y is y = 202x.

Example 5 :

Determine the constant of proportionality for each table.

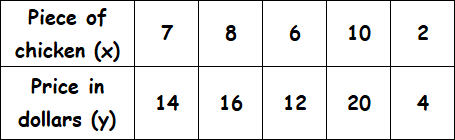
Solution :

To find the constant of proportionality, we have to divide y by x.

Ratio of y to x :

14/7 = 2

16/8 = 2

12/6 = 2

20/10 = 2

4/2 = 2

The ratio for each pair of x- and y-values is 2. So, the variables have a proportional relationship.

For each piece of chicken it costs 2 dollars. 

A proportional relationship between x and y can be modeled by the equation y = kx.

Here the value of k is 2.

So, the required equation for the relationship between  x and y is y = 2x.

Example 6 :

Determine the constant of proportionality for each table.

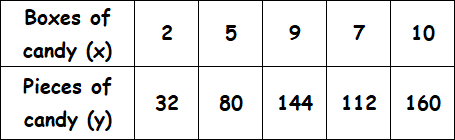
Solution :

To find the constant of proportionality, we have to divide y by x.

Ratio of y to x :

32/2 = 16

80/5 = 16

144/9 = 16

112/7 = 16

160/10 = 16

The ratio for each pair of x- and y-values is 16. So, the variables have a proportional relationship.

For every box of candy you get 16 pieces.

A proportional relationship between x and y can be modeled by the equation y = kx.

Here the value of k is 16.

So, the required equation for the relationship between  x and y is y = 16x.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.