WRITE THE PRODUCT IN EXPONENTIAL FORM

Exponents are used to avoid the repetition of writing the same numerical values many times.

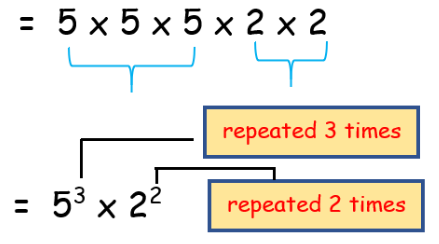
Write each number in exponent form :

Example 1 :

2 × 2 × 3 × 3 × 3

Solution :

2 × 2 × 3 × 3 × 3

2 is repeated 2 times and 3 is repeated 3 times.

=  2² × 3³

Example 2 :

2 × 5 × 5

Solution :

2 × 5 × 5

2 is repeated once and 5 is repeated 2 times.

=  2 × 5²

Example 3 :

2 × 3 × 3 × 3 × 5

Solution :

2 × 3 × 3 × 3 × 5

2 and 5 are repeated once and 3 is repeated 3 times. 

=  2 × 3³ × 5

Example 4 :

5 × 5 × 7 × 7

Solution :

5 × 5 × 7 × 7

5 is repeated twice and 7 is repeated twice.

=  5² × 7²

Example 5 :

2 × 2 × 5 × 5 × 5 × 7

Solution :

2 × 2 × 5 × 5 × 5 × 7

2 is repeated twice, 5 is repeated 3 times and 7 is repeated once.

=  2² × 5³ × 7

Example 6 :

3 × 3 × 7 × 7 × 11 × 11

Solution :

3 × 3 × 7 × 7 × 11 × 11

3, 7 and 11 are repeated twice.

=  3² × 7² × 11²

Example 7 :

56

Solution :

Since 56 is a composite number, we can decompose it into prime factors.

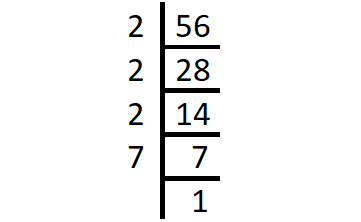
Prime factorization of 56 :

56  =  2 x 2 x 2 x 7

2 is repeated 3 times and 7 is repeated once.

=  2³ x 7

Example 8 :

24

Solution :

By decomposing 24 as prime factors, we get

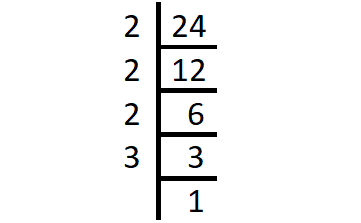
Prime factorization of 24 :

24  =  2 x 2 x 2 x 3

2 is repeated 3 times and 3 is repeated once.

=  2³ x 3

Example 9 :

108

Solution :

By decomposing 108 as prime factors, we get

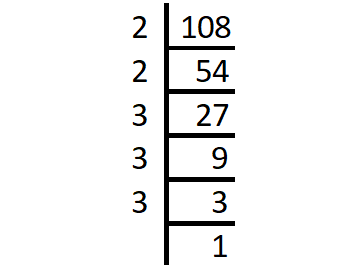
Prime factorization of 108 :

108  =  2 x 2 x 3 x 3 x 3

2 is repeated 2 times and 3 is repeated 3 times.

=  2² x 3³

Example 10 :

80

Solution :

By decomposing 80 as prime factors, we get

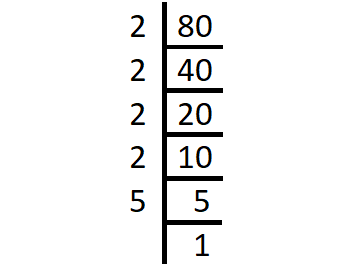
Prime factorization of 80 :

80  =  2 x 2 x 2 x 2 x 5

2 is repeated 4 times and 5 is repeated once.

=  2⁴ x 5

Example 11 :

8³ x 8⁴ is equal to

a)  8¹²       b)  64⁷      c)  2²¹    d)  None of these

Solution :

= 8³ x 8⁴

When we have two which are multiplied, we get

= 8³⁺⁴

= 8⁷

Example 12 :

Which of the following is equal to

3 x 3 x 3 x 3 x 3 x 3

a)  3⁶       b)  18      c)  9³    d)  729

Solution :

= 3 x 3 x 3 x 3 x 3 x 3

Here 3 is multiplied six times, to convert into exponential form, we get

= 8⁶

Example 13 :

(4²)³

a)  4⁸       b)  4⁶      c)  4⁵    d)  4²³

Solution :

(4²)³

When we have power raised by another power, we have to multiply the powers.

= 4^(2x3)

= 4⁶

Example 14 :

2.7 x 10^-3 is equal to

a)  0.000027       b)  0.00027      c)  0.0027    d)  2.007

Solution :

2.7 x 10^-3

Converting the negative exponent to positive exponent, we get

= 2.7 x (1/10³)

= 2.7/10³

= 2.7/1000

Moving the decimal 3 digits to the left. We get

= 0.0027

So, option c is correct.

Example 15 :

(-1)¹⁰⁰¹ is equal to

a)  1      b)  -1      c)  1001    d)  0

Solution :

(-1)¹⁰⁰¹ 

1001 is odd number, multiplying -1 odd number of times. We get -1 as result. So, option b is correct.

Example 16 :

The value of (-2)⁵ is equal to

a)  -32      b)  10      c)  1/32    d)  -1/32

Solution :

(-2)⁵

Since we have negative base and multiplying this odd number of times, we get the answer with negative sign.

= -32

So, option a is correct.

Example 17 :

Express 2 x 3 x 2 x 3 x 2 x 3 x 2 x 3 in exponential form.

Solution :

= 2 x 3 x 2 x 3 x 2 x 3 x 2 x 3

Here 2 is multiplied four times and 3 is multiplied four time. Writing it in exponential form, we get

= 2⁴ x 3⁴

= (2 x 3)⁴

= 6⁴

Example 18 :

Express 7⁹ in the product form.

Solution :

= 7⁹

Since we have 9 at the power, we have to repeat the base nine times.

= 7 x 7 x 7 x 7 x 7 x 7 x 7 x 7 x 7

Example 18 :

Express (3/4)³ in the form of p/q.

Solution :

= (3/4)³

= (3 x 3 x 3)/(4 x 4 x 4)

= 27/64

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.