WRITING AN EQUATION FROM A TABLE

Example 1 :

Elizabeth’s cell phone plan lets her choose how many minutes are included each month. The table shows the plan’s monthly cost y for a given number of included minutes x. Write an equation in slope-intercept form to represent the situation.

Solution :

Step 1 : 

Notice that the change in cost is the same for each increase of 100 minutes. So, the relationship is linear.

Step 2 : 

Choose any two points in the form (x, y), from the table to find the slope :

For example, let us choose (100, 14) and (200, 20).

Use the slope formula. 

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (100, 14) for (x₁, y₁) and (200, 20) for (x₂, y₂).

m  =  (20 - 14) / (200 - 100)

m  =  6 / 100

m  =  0.06

Step 3 : 

Find the y-intercept using the slope and any point from the table.

Slope-intercept form equation of a line :

y  =  mx + b

Plug m  =  0.06, and (x, y)  =  (100, 14)

14  =  0.06(100) + b

14  =  6 + b

8  =  b

Step 4 : 

Now, plug m = 0.06 and b = 8 in slope-intercept form equation of a line.

y  =  mx + b

y  =  0.06x + 8

Example 2 :

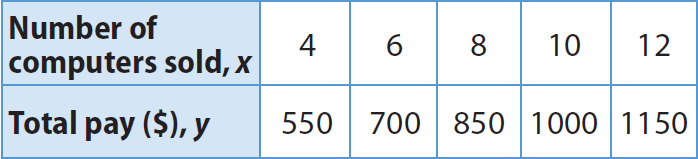
A salesperson receives a weekly salary plus a commission for each computer sold. The table shows the total pay, y, and the number of computers sold, x. Write an equation in slope-intercept form to represent this situation.

Solution :

Step 1 : 

Notice that the change in total pay is the same for increase in sales of every 2 computers. So, the relationship is linear.

Step 2 : 

Choose any two points in the form (x, y), from the table to find the slope :

For example, let us choose (4, 550) and (6, 700).

Use the slope formula. 

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute (4, 550) for (x₁, y₁) and (6, 700) for (x₂, y₂).

m  =  (700 - 550) / (6 - 4)

m  =  150 / 2

m  =  75

Step 3 : 

Find the y-intercept using the slope and any point from the table.

Slope-intercept form equation of a line :

y  =  mx + b

Plug m  =  75, and (x, y)  =  (4, 550)

550  =  75(4) + b

550  =  300 + b

250  =  b

Step 4 : 

Now, plug m = 75 and b = 250 in slope-intercept form equation of a line.

y  =  mx + b

y  =  75x + 250

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.