WRITING EQUATIONS OF CIRCLES IN STANDARD FORM FROM GRAPHS

Example 1 :

Write the equation of the circle in standard form from the graph given below.

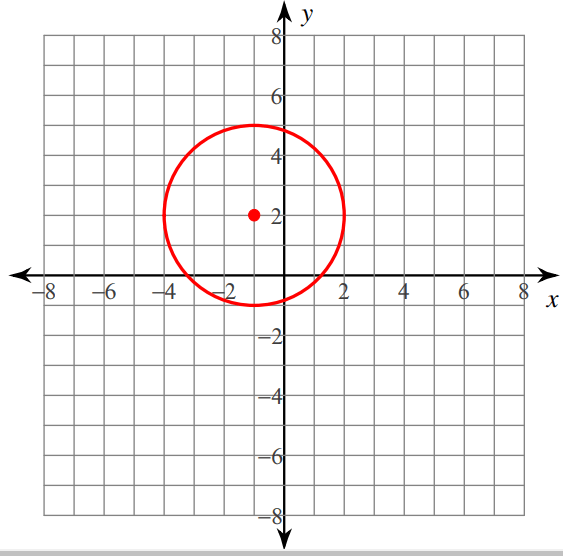
Solution :

From the given graph, first let us mark the center point. Here (-1, 2) is the center point

(h, k)  ==> (1, 2)

One of the points lies on the circle is (2, 2).

Let us find the distance between the points (1, 2) and (2, 2)

d = √(x₂-x₁)² + (y₂ - y₁)²

d = √(2 - 1)² + (2 - 2)²

d = √1² + 0²

d = 1 unit

Standard equation of the circle

(x - h)² + (y - k)²  = r²

(x - 1)² + (y - 2)²  = 1²

(x - 1)² + (y - 2)²  = 1

Example 2 :

Write the equation of the circle in standard form from the graph given below.

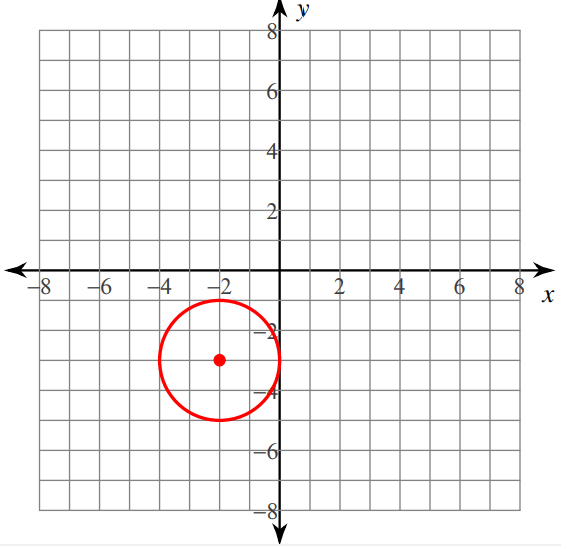
Solution :

From the given graph, first let us mark the center point.

Here (-2, -3) is the center point.

(h, k)  ==> (-2, -3)

One of the points lies on the circle is (-2, -1)

Let us find the distance between the points (-2, -3) and (-2, -1)

d = √(x₂-x₁)² + (y₂ - y₁)²

d = √(-2 - (-2))² + (-1 - (-3))²

d = √(-2 + 2)² + (-1 + 3)²

d = √0² + 2²

d = √4

d = 2 units

Standard equation of the circle

(x - (-2))² + (y - (-3))²  = 2²

(x + 2)² + (y + 3)²  =  2²

(x + 2)² + (y + 3)²  = 4

Example 3 :

Write the equation of the circle in standard form from the graph given below.

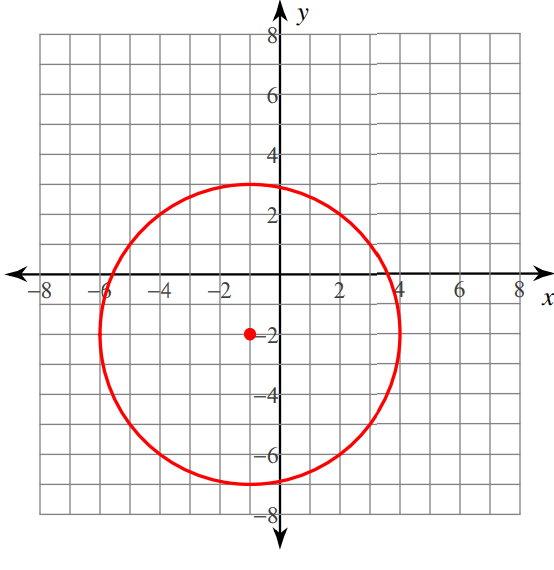
Solution :

From the given graph, first let us mark the center point.

Here (-1, -2) is the center point.

(h, k)  ==> (-1, -2)

One of the points lies on the circle is (-1, -7)

Let us find the distance between the points (-1, -2) and (-1, -7)

d = √(x₂-x₁)² + (y₂ - y₁)²

d = √(-7 - (-2))² + (-1 - (-1))²

d = √(-7 + 2)² + (-1 + 1)²

d = √(-5)² + 0²

d = √25

d = 5 units

Standard equation of the circle

(x - (-1))² + (y - (-2))²  = 5²

(x + 1)² + (y + 2)²  =  25

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.