WRITING EQUIVALENT EXPRESSIONS USING DISTRIBUTIVE PROPERTY WORKSHEET

Problem 1 :

Use distributive property to write an expression that is equivalent to 3(10 + 2).

Problem 2 :

Use distributive property to write an expression that is equivalent to 5(6 - 3).

Problem 3 :

Use distributive property to write an expression that is equivalent to  7(x - 3).

Problem 4 :

Use distributive property to write an expression that is equivalent to 2(2x - 5). 

Solution :

2(2x - 5)  =  2(2x) - 2(5)

2(2x - 5)  =  4x - 10

Problem 5 :

Use distributive property to write an expression that is equivalent to 3(x - 5).

Problem 6 :

Use distributive property to write an expression that is equivalent to 5x + 25.

Problem 7 :

Use distributive property to write an expression that is equivalent to 7y + 5y.

Problem 8 :

Use distributive property to write an expression that is equivalent to 0.2y + z.

Detailed Answer Key

Problem 1 :

Use distributive property to write an expression that is equivalent to 3(10 + 2).

Solution : 

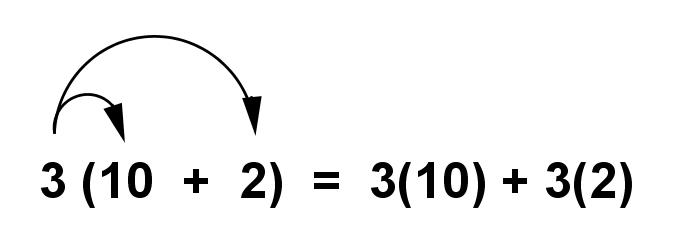
Problem 2 :

Use distributive property to write an expression that is equivalent to 5(6 - 3).

Solution : 

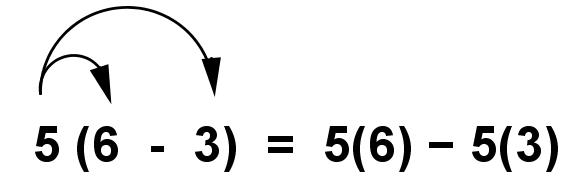
Problem 3 :

Use distributive property to write an expression that is equivalent to  7(x - 3).

Solution :

7(x - 3)  =  7x - 7(3)

7(x - 3)  =  7x - 21

Problem 4 :

Use distributive property to write an expression that is equivalent to 2(2x - 5). 

Solution :

2(2x - 5)  =  2(2x) - 2(5)

2(2x - 5)  =  4x - 10

Problem 5 :

Use distributive property to write an expression that is equivalent to 3(x - 5).

Solution :

3(x - 5)  =  3x - 3(5)

3(x - 5)  =  3x - 15

Problem 6 :

Use distributive property to write an expression that is equivalent to 5x + 25.

Solution :

5x + 25  =  5x + 5(5)

5x + 25  =  5(x + 5)

Problem 7 :

Use distributive property to write an expression that is equivalent to 7y + 5y.

Solution :

7y + 5y  =  y(7 + 5)

Problem 8 :

Use distributive property to write an expression that is equivalent to 0.2y + z.

Solution :

0.2y + z  =  0.2y + 1z

0.2y + z  =  0.2y + 0.2(5z)

0.2y + z  =  0.2(y + 5z)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.