WRITING FUNCTIONS
The amount of money Ryan earns is $7 times the number of hours he works. Write an equation using two different variables to show this relationship.
Amount earned
is
$7
times
the number of hours worked
y
=
$7
⋅
x
Ryan can use this equation to find how much money she will earn for any number of hours he works.
Using a Table to Write an Equation
Example 1 :
Determine a relationship between the x- and y-values. Write an equation.
Solution :
Step 1 :
List possible relationships between the first x- and y-values.
1 - 3 = -2 or 1(-2) = -2
Step 2 :
Determine if one relationship works for the remaining values.
|
2 - 3 = -1 ✓ 3 - 3 = 0 ✓ 4 - 3 = 1 ✓ |
2(-2) ≠ -1 ✗ 3(-2) ≠ 0 ✗ 4(-2) ≠ 1 ✗ |
The first relationship works. The value of y is 3 less than x.
Step 3 :
Write an equation.
y = x - 3 The value of y is 3 less than x.
The equation in the above example describes a function because for each x-value (input), there is only one y-value (output).
The input of a function is the independent variable. The output of a function is the dependent variable. The value of the dependent variable depends on, or is a function of, the value of the independent variable. For Tasha, the amount she earns depends on, or is a function of, the amount of time she works.
Identifying Independent and Dependent Variables
Identify the independent and dependent variables in each situation.
Example 2 :
In the winter, more electricity is used when the temperature goes down, and less is used when the temperature rises.
Solution :
The amount of electricity used depends on the temperature.
Dependent : Amount of electricity
Independent : Temperature
Example 3 :
The cost of shipping a package is based on its weight.
Solution :
The cost of shipping a package depends on its weight.
Dependent : Cost
Independent : Weight
Example 4 :
The faster Ron walks, the quicker he gets home.
Solution :
The time it takes Ron to get home depends on the speed he walks.
Dependent : Time
Independent : Speed
An algebraic expression that defines a function is a function rule. (7 · x) in the equation about Ryan’s earnings is a function rule.
If x is the independent variable and y is the dependent variable, then function notation for y is f (x) , read “f of x,” where f names the function. When an equation in two variables describes a function, you can use function notation to write it.
The dependent variable
is
a function of
the independent variable
y
is
a function of
x
y
=
f
(x)
Since y = f(x), Ryan’s earnings, y = 7x, can be rewritten in function notation by substituting f(x) for y :
f(x) = 7x
Sometimes functions are written using y, and sometimes functions are written using f(x).
Writing Functions
Identify the independent and dependent variables. Write an equation in function notation for each situation.
Example 5 :
A lawyer’s fee is $120 per hour for his services.
Solution :
The fee for the lawyer depends on how many hours he works.
Dependent : Fee
Independent : Hours
Let h represent the number of hours the lawyer works.
The function for the lawyer’s fee is
f(h) = 120h
Example 6 :
The admission fee to a local carnival is $10. Each ride costs $2.50.
Solution :
The total cost depends on the number of rides ridden, plus $10.
Dependent : Total cost
Independent : Number of rides
Let r represent the number of rides ridden.
The function for the total cost of the carnival is
f(r) = 2.50r + 10
You can think of a function as an input-output machine. For Tasha’s earnings, f(x) = 7x, if you input a value x, the output is 7x.
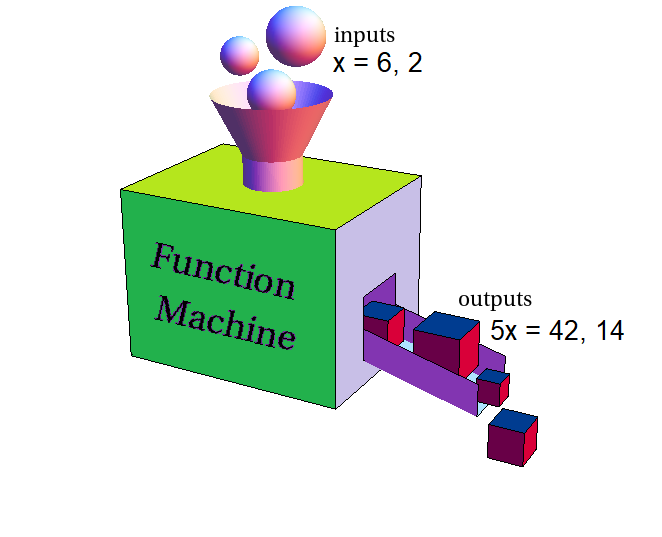
If Ryan wanted to know how much money he would earn by working 6 hours, she could input 6 for x and find the output. This is called evaluating the function.
Evaluating Functions
Evaluate each function for the given input values.
Example 7 :
For f(x) = 4x, find f(x) when x = 5 and when x = 6.5.
Solution :
|
f(x) = 4x Substitute 5 for x. f(4) = 4(5) = 20 |
f(x) = 4x Substitute 6.5 for x. f(6.5) = 4(6.5) = 26 |
Example 8 :
For g(y) = 3y + 5, find g(y) when y = 2.5 and when y = -2.
Solution :
|
g(y) = 3y + 5 Substitute 2.5 for y. g(2.5) = 3(2.5) + 5 = 7.5 + 5 = 12.5 |
g(y) = 3y + 5 Substitute -2 for y. g(-2) = 3(-2) + 5 = -6 + 5 = -1 |
Example 9 :
For h(t) = 0.5t - 4, find h(t) when t = 4 and when t = -8.
Solution :
|
h(t) = 0.5t - 4 Substitute 4 for t. h(4) = 0.5(4) - 4 = 2 - 4 = -2 |
h(t) = 0.5t - 4 Substitute -8 for t. h(-8) = 0.5(-8) - 4 = -4 - 4 = -8 |
Finding the Reasonable Domain and Range of a Function
Example 10 :
Alex has already sold $24 worth of tickets to the school play. He has 5 tickets left to sell at $3 per ticket. Write a function to describe how much money Manuel can collect from selling tickets. Find the reasonable domain and range for the function.
Solution :
Money collected from ticket sales is $3 per ticket plus the $24 already sold.
f(x) = $3 ⋅ x + 24
f(x) = 3x + 24
If he sells x more tickets, he will collect f(x) = 3x + 24 dollars.
Alex has only 5 tickets left to sell, so he could sell 0, 1, 2, 3, 4 or 5 tickets.
A reasonable domain is
{0, 1, 2, 3, 4, 5}
Substitute these values into the function rule to find the range values.
|
x 0 1 2 3 4 5 |
f(x) 24 27 30 33 36 39 |
The reasonable range for this situation is
{$24, $27, $30, $33, $36, $39}
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Solving Trigonometric Equations Problems and Solutions
Dec 18, 24 10:53 AM
Solving Trigonometric Equations Problems and Solutions -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Dec 17, 24 10:13 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 88)
Dec 17, 24 10:07 AM
Digital SAT Math Problems and Solutions (Part - 88)
