WRITING LINEAR EQUATIONS FROM SITUATIONS AND GRAPHS WORKSHEET

Problem 1 : 

The rent charged for space in an office building is a linear relationship related to the size of the space rented.At west main street office rentals, $750 rent charged for 600 square feet of space and $1150 rent charged for 900 square feet of space. Write an equation in slope-intercept form for the rent at West Main Street Office Rentals.

Problem 2 :

Hari’s weekly allowance varies depending on the number of chores he does. He received $16 in allowance the week he did 12 chores, and $14 in allowance the week he did 8 chores. Write an equation for his allowance in slope-intercept form.

Problem 3 :

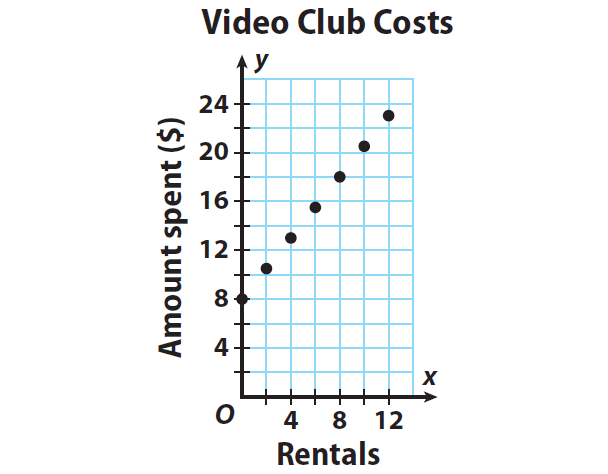
A video club charges a one-time membership fee plus a rental fee for each DVD borrowed. Use the graph to write an equation in slope-intercept form to represent the amount spent, y, on x DVD rentals.

Problem 4 :

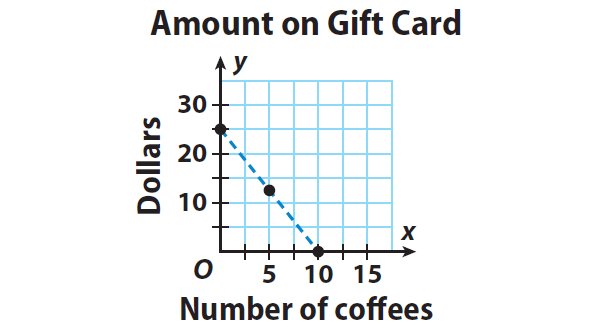
The cash register subtracts $2.50 from a $25 Coffee Café gift card for every medium coffee the customer buys. Use the graph to write an equation in slope-intercept form to represent this situation.

Answers

Problem 1 :

The rent charged for space in an office building is a linear relationship related to the size of the space rented.At west main street office rentals, $750 rent charged for 600 square feet of space and $1150 rent charged for 900 square feet of space. Write an equation in slope-intercept form for the rent at West Main Street Office Rentals.

Answer :

Step 1 :

Identify the independent and dependent variables.

The independent variable (x) is the square footage of floor space.

The dependent variable (y) is the monthly rent.

Step 2 :

Write the information given in the problem as ordered pairs.

The rent for 600 square feet of floor space is $750 :

(600, 750)

The rent for 900 square feet of floor space is $1150 :

(900, 1150)

Step 3 : 

Find the slope.  

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute : 

(x₁, y₁)  =  (600, 750)

(x₂, y₂)  =  (900, 1150)

Then, 

m  =  (1150 - 750) / (900 - 600)

m  =  400 / 300

m  =  4/3

Step 4 : 

Find the y-intercept.

Use the slope 4/3 and one of the ordered pairs (600, 750).

Slope-intercept form : 

y  =  mx + b

Substitute  m = 4/3,  x = 600 and y = 750.  

750  =  (4/3)(600) + b

750  =  (4)(200) + b

750  =  800 + b

-50  =  b

Step 5 : 

Substitute the slope and y-intercept.

Slope-intercept form

y  =  mx + b 

Substitute  m = 4/3 and b = -50

y  =  (4/3)x + (-50)

y  =  (4/3)x - 50

Problem 2 :

Hari’s weekly allowance varies depending on the number of chores he does. He received $16 in allowance the week he did 12 chores, and $14 in allowance the week he did 8 chores. Write an equation for his allowance in slope-intercept form.

Answer :

Step 1 :

Identify the independent and dependent variables.

The independent variable (x) is number of chores Hari does per week

The dependent variable (y) is the allowance he receives per week. 

Step 2 :

Write the information given in the problem as ordered pairs.

For 12 chores, he receives  $16 allowance : 

(12, 16)

For 8 chores, he receives  $14 allowance : 

(8, 14)

Step 3 : 

Find the slope.  

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute : 

(x₁, y₁)  =  (12, 16)

(x₂, y₂)  =  (8, 14)

Then, 

m  =  (14 - 16) / (8 - 12)

m  =  (-2) / (-4)

m  =  1/2

m  =  0.5

Step 4 : 

Find the y-intercept.

Use the slope 0.5 and one of the ordered pairs (8, 14).

Slope-intercept form : 

y  =  mx + b

Substitute  m = 0.5,  x = 8 and y = 14.  

14  =  (0.5)(8) + b

14  =  4 + b

10  =  b

Step 5 : 

Substitute the slope and y-intercept.

Slope-intercept form

y  =  mx + b 

Substitute  m = 0.5 and b = 10

y  =  0.5x + 10

Problem 3 :

A video club charges a one-time membership fee plus a rental fee for each DVD borrowed. Use the graph to write an equation in slope-intercept form to represent the amount spent, y, on x DVD rentals.

Answer :

Step 1 :

Choose two points on the graph, (x₁, y₁) and (x₂, y₂), to find the slope.

Find the ratio between change in y-values and change in x-

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute : 

(x₁, y₁)  =  (0, 8)

(x₂, y₂)  =  (8, 18)

Then, 

m  =  (18 - 8) / (8 - 0)

m  =  10 / 8

m  =  1.25

Step 2 : 

Read the y-intercept from the graph. That is, the point at which the line cuts y-axis.   

The y-intercept is 8.

b  =  8

Step 3 : 

Let us use slope (m) and y-intercept (b) values to write an equation in slope-intercept form.

y  =  mx + b (Slope-intercept form)

Substitute  m  =  1.25 and b  =  8. 

y  =  1.25x + 8

Problem 4 :

The cash register subtracts $2.50 from a $25 Coffee Café gift card for every medium coffee the customer buys. Use the graph to write an equation in slope-intercept form to represent this situation.

Answer :

Step 1 :

Choose two points on the graph, (x₁, y₁) and (x₂, y₂), to find the slope.

Find the ratio between change in y-values and change in x-

m  =  (y₂ - y₁) / (x₂ - x₁)

Substitute : 

(x₁, y₁)  =  (0, 25)

(x₂, y₂)  =  (10, 0)

Then, 

m  =  (0 - 25) / (10 - 0)

m  =  -25 / 10

m  =  -2.5

Step 2 : 

Read the y-intercept from the graph. That is, the point at which the line cuts y-axis.   

The y-intercept is 25.

Step 3 : 

Let us use slope (m) and y-intercept (b) values to write an equation in slope-intercept form.

y  =  -2.5x + 25 (Slope-intercept form)

Substitute  m  =  -2.5 and b  =  25. 

y  =  -2.5x + 25

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.