WRITING RATIO OF SHADED TO UNSHADED AREA

Example 1 :

In each of the following diagrams:

i) Find the ratio of the shaded area to the unshaded area.

ii) Find the ratio of the shaded area to the total area.

iii)  Find the fraction of the total area which is shaded

Solution :

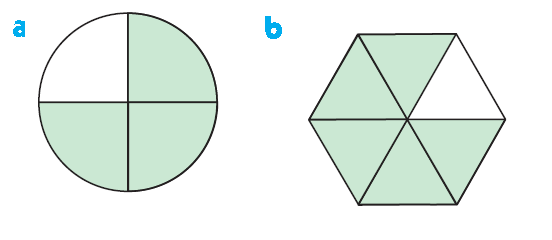
(a) 

(i)  In the first picture out of 4 equal parts, only 3 of them are shaded.

Ratio of shaded to unshaded  =  3 : 1

(ii) Ratio of shaded to total area  =  3 : 4

(iii)  Fractional form of shaded region  =  3/4.

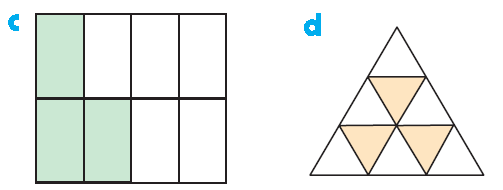
(b) 

(i)  In the first picture out of 6 equal parts, only 5 of them are shaded.

Ratio of shaded to unshaded  =  5 : 1

(ii) Ratio of shaded to total area  =  5 : 6

(iii)  Fractional form of shaded region  =  5/6.

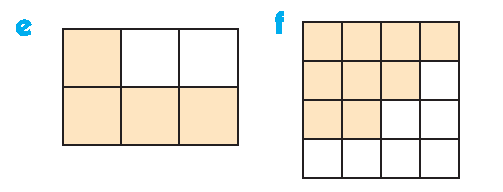
(c) 

(i)  In the first picture out of 8 equal parts, only 3 of them are shaded.

Ratio of shaded to unshaded  =  3 : 5

(ii) Ratio of shaded to total area  =  3 : 8

(iii)  Fractional form of shaded region  =  3/8.

(d) 

(i)  In the first picture out of 9 equal parts, only 3 of them are shaded.

Ratio of shaded to unshaded  =  3 : 6

(ii) Ratio of shaded to total area  =  3 : 9

Since, it can be simplified the answer is 1 : 3

(iii)  Fractional form of shaded region  =  3/9 or 1/3.

(e) 

(i)  In the first picture out of 6 equal parts, only 4 of them are shaded.

Ratio of shaded to unshaded  =  4 : 2

(ii) Ratio of shaded to total area  =  4 : 6

Since, it can be simplified the answer is 2 : 3

(iii)  Fractional form of shaded region  =  4/6 (or) 2/3

(f)  

(i)  In the first picture out of 16 equal parts, only 9 of them are shaded.

Ratio of shaded to unshaded  =  9 : 7

(ii) Ratio of shaded to total area  =  9 : 16

(iii)  Fractional form of shaded region  =  9/16.

Example 2 :

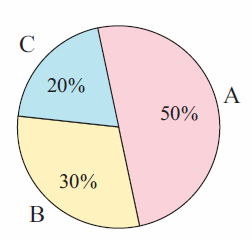
The pie chart represents the sales of three different types of soap powders, A, B and C.

a) Write as a ratio :

i) the sales of A to the sales of B.

ii) the sales of A to the total sales.

b) What fraction of the total sales made is the sales of brand A?

Solution :

i)  50% : 30%

By simplifying we get, 5 : 3.

ii)  Sales of A is 50 and total sales is 100.

=  50 : 100

=  1 : 2

(b)  50/100 (or) 1/2.

Example 3 :

A map scale is 1 : 50 000. Rates and Ratios

(i) How far is the real life distance in kilometres if the map distance is 5cm?

Since the scale is 1 : 50 000 then 5cm on the map is a real life distance of:

50 000 × 5 cm = 250 000 cm = 2.5 km.

(ii) If the real life distance is 7 km, how many centimeters is this on the map?

7 km = 7000 m = 700 000 cm

For each 50 000cm in real life it will be 1cm on the map. `

Therefore, 700000 / 50000 = 14 cm

Therefore on the map the distance is 14 cm.

Example 4 :

The real life distance between Alpha Town and Beta Town is 3 km.

(i) Find the scale of this map given that each grid unit is 1cm. The scale is the ratio 4 grid units to 3km.

(ii) Using this map scale, find the distance between Beta Town and Gamma Town.

Solution :

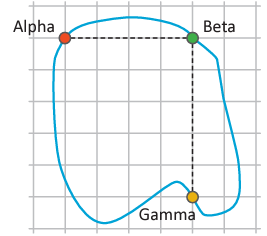
(i) 

4cm : 3km = 4 cm : 300 000cm

= 4 : 300 000

= 1 : 75 000

1 km = 100000 cm.

ii)  

The distance between Beta and Gamma towns on the map is 5 grid units and therefore 5 cm.

Therefore the real life difference is:

5 × 75 000cm = 375 000cm

Example 5 :

Sleeping time of a Python in a 24 hours clock represented by the shaded portion.

Find the ratio of sleeping time to awaking time .

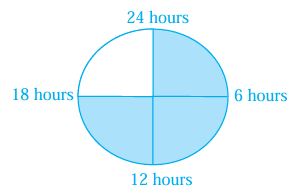
Solution :

Shaded parts = 3/4

Total number of hours = 24

3/4 of 24 is sleeping time and 1/4 of 24 is awaking time.

Sleeping time = (3/4) x 24

= 18

Awaking time = (1/4) x 24

= 6

The ratio between sleeping time to awaking time = 18 : 16

= 3 : 1

Example 6 :

In a floral design made from tiles each of dimensions 40 cm by 60 cm, find the ratios of:

(a) the perimeter of shaded portion to the perimeter of the unshaded design.

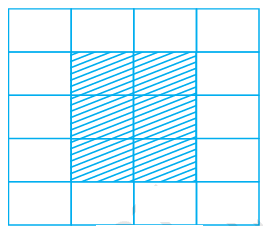
Solution :

By observing the picture,

length of each rectangle = 40 cm

width = 60 cm

length of shaded portion = 40 + 40 ==> 80 cm

width of shaded portion = 60 + 60 + 60 ==> 180 cm

Perimeter of shaded portion = 2(80 + 180)

= 2(260)

= 520

Perimeter of unshaded = 14(80+60)

= 1960

Ratio between shaded to unshaded = 520 : 1960

= 520/1960

= 26 : 98

= 13 : 49

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.