WRITING RATIONAL NUMBERS AS DECIMALS

A rational number is a number that can be written as a ratio of two integers a and b, where b is not zero. For example, 4/7 is a rational number, as is 0.37 because it can be written as the fraction.

Example 1 : 

Write the rational number -5/16 as a decimal. 

Solution : 

Divide 5 by 16.

Step 1 :

Take decimal point after 5.

Step 2 :

Add a zero after the decimal point.

Step 3 : 

In 50, there are three 16's which is 48. So, subtract 48 from 50. Use the grid to help you complete the long division.

Add zeros in the dividend and continue dividing until the remainder is 0.

The above explained process has been illustrated in the picture given below. 

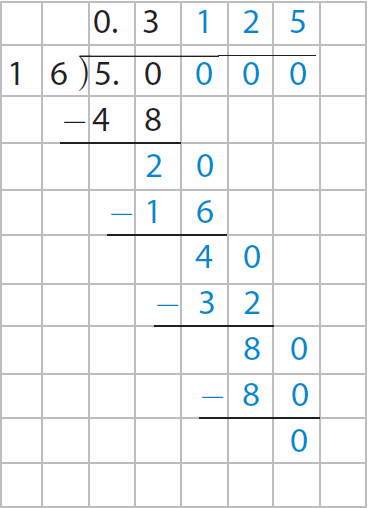
So, the decimal equivalent of -5/16 is - 0.3125.

Example 2 : 

Write the rational number 13/33 as a decimal. 

Solution : 

Divide 13 by 33.

Step 1 :

Take decimal point after 13.

Step 2 :

Add a zero after the decimal point.

Step 3 : 

In 130, there are three 33's which is 99. So, subtract 99 from 130. Use the grid to help you complete the long division.

Write the quotient with its repeating pattern and indicate that the repeating numbers continue.

The above explained process has been illustrated in the picture given below. 

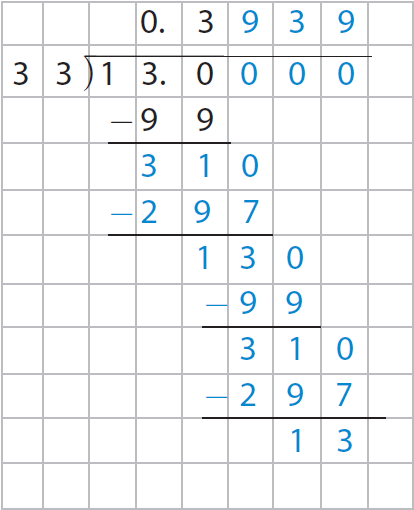
So, the decimal equivalent of 13/33 is  0.3939..................

Example 3 : 

Write the rational number 60/75 as a decimal. 

Solution : 

Divide 60 by 75.

Step 1 :

Take decimal point after 60.

Step 2 :

Add a zero after the decimal point.

Step 3 : 

In 600, there are eight 75's which is 600. So, subtract 600 from 600. 

When we do so, we get the remainder 0.

The above explained process has been illustrated in the picture given below. 

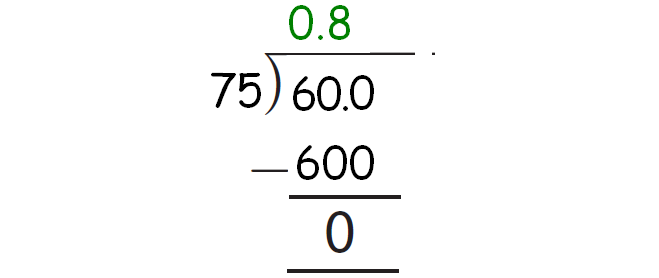
So, the decimal form the rational number 60/75 is 0.8. 

Example 4 : 

Write the rational number 6 3/4 as a decimal. 

Solution : 

Take the fractional part 3/4

Divide 3 by 4.

Step 1 :

Take decimal point after 3.

Step 2 :

Add a zero after the decimal point.

Step 3 : 

In 30, there are seven 4's which is 28. So, subtract 28 from 30. Use the grid to help you complete the long division.

Add zeros in the dividend and continue dividing until the remainder is 0.

The above explained process has been illustrated in the picture given below. 

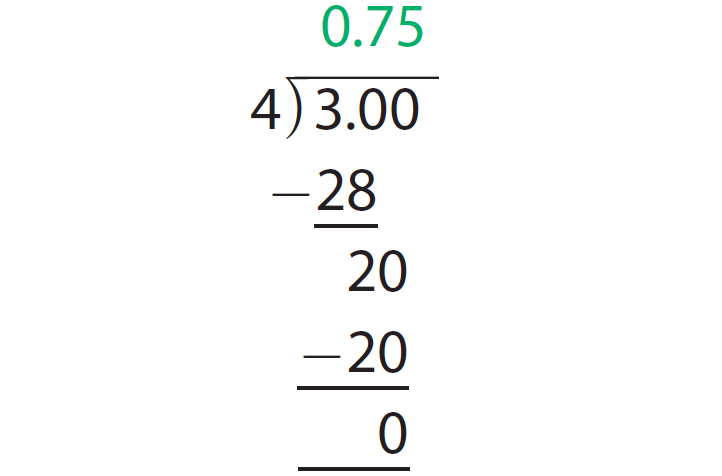
The decimal equivalent to the fractional part 3/4 is 0.75.

Rewrite the mixed number as the sum of the whole part and the decimal part.

6 3/4  =  6 + 3/4

6 3/4  =  6 + 0.75

6 3/4  =  6.75

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.