X AND Y INTERCEPTS WORKSHEET

Problems 1-4 : Find the x- and y-intercepts.

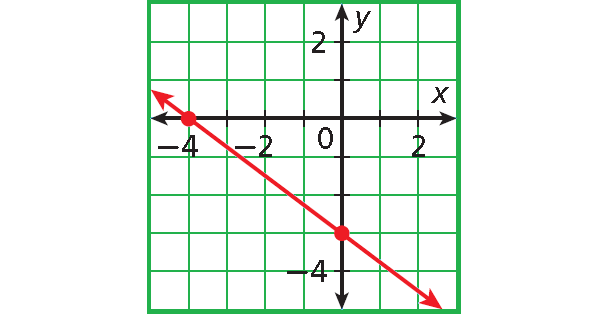
Problem 1 :

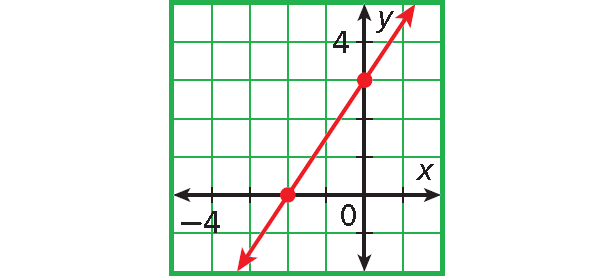
Problem 2 :

Problem 3 :

3x - 2y = 12

Problem 4 :

5y = 3x + 30

Problems 5-9 : Use intercepts to graph the line described by each equation.

Problem 5 :

2x - 4y = 8

Problem 6 :

y = x/4 + 1

Problem 7 :

2x - y = 4

Problem 8 :

2x + 3y + 6 = 0

Problem 9 :

2y = 12 - 3x/2

Problem 10 :

A tramway travels a distance of about 4500 meters to the top of the peak. Its rate is 300 meters per minute. The function f(x) = 4500 - 350x gives the tram’s distance in meters from the top of the peak after x minutes. Graph this function and find the intercepts. What does each intercept represent?

Answers

1. Answer :

The graph intersects the x-axis at (-4, 0).

The x-intercept is -4.

The graph intersects the y-axis at (0, -3).

The y-intercept is -3.

2. Answer :

The graph intersects the x-axis at (-2, 0).

The x-intercept is -2.

The graph intersects the y-axis at (0, 4).

The y-intercept is 4.

3. Answer :

To find the x-intercept, replace y with 0 and solve for x.

3x - 2y = 12

3x - 2(0) = 12

3x - 0 = 12

3x = 12

3x/3 = 12/3

x = 4

The x-intercept is 4.

To find the y-intercept, replace x with 0 and solve for y.

3x - 2y = 12

3(0) - 2y = 12

0 - 2y = 12

-2y = 12

-2y/(-2) = 12/(-2)

y = -6

The y-intercept is -6.

4. Answer :

To find the x-intercept, replace y with 0 and solve for x.

5y = 3x + 30

5(0) = 3x + 30

0 = 3x + 30

-30 = 3x

-30/3 = 3x/3

-10 = x

The x-intercept is -10.

To find the y-intercept, replace x with 0 and solve for y.

5y = 3x + 30

5y = 3(0) + 30

5y = 0 + 30

5y = 30

5y/5 = 30/5

y = 6

The y-intercept is 6.

5. Answer :

Step 1 :

Find the intercepts.

x-intercept :

2x - 4y = 8

2x - 4(0) = 8

2x - 0 = 8

2x = 8

2x/2 = 8/2

x = 4

(4, 0)

y-intercept :

2x - 4y = 8

2(0) - 4y = 8

0 - 4y = 8

-4y = 8

-4y/(-4) = 8/(-4)

y = -2

(0, -2)

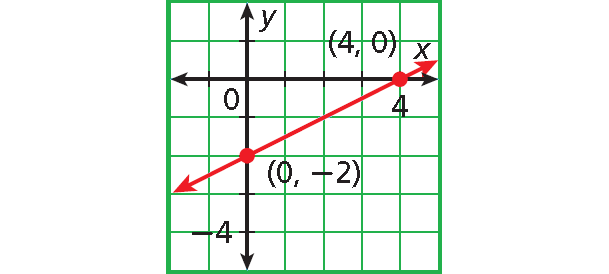
Step 2 :

Plot (4, 0) and (0, -2).

Connect with a straight line.

6. Answer :

Step 1 :

Find the intercepts.

x-intercept :

y = x/4 + 1

0 = x/4 + 1

-1 = x/4

-4 = x

(-4, 0)

y-intercept :

y = x/4 + 1

y = 0/4 + 1

y = 0 + 1

y = 1

(0, 1)

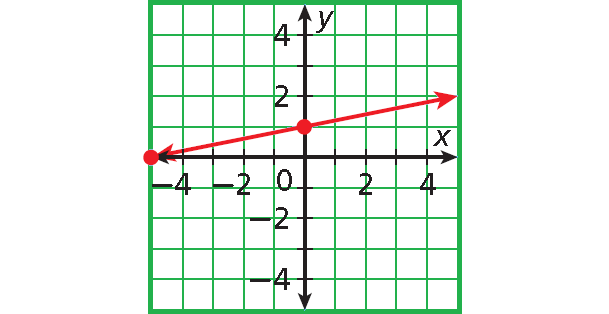
Step 2 :

Plot (-4, 0) and (0, 1).

Connect with a straight line.

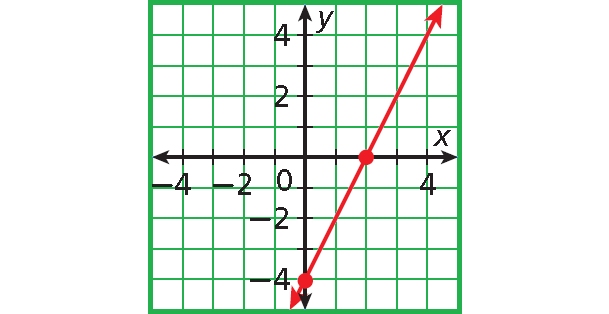
7. Answer :

Step 1 :

Find the intercepts.

x-intercept :

2x - y = 4

2x - 0 = 4

2x = 4

2x/2 = 4/2

x = 2

(2, 0)

y-intercept :

2x - y = 4

2(0) - y = 4

0 - y = 4

-y = 4

y = -4

(0, -4)

Step 2 :

Plot (2, 0) and (0, -4).

Connect with a straight line.

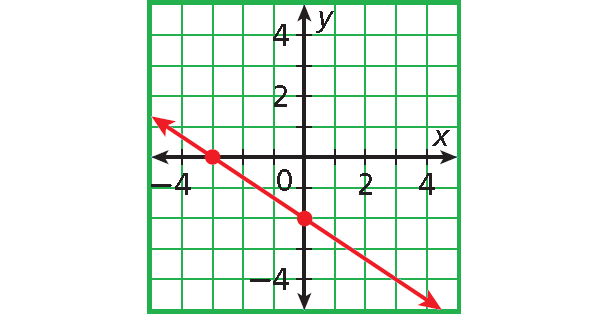
8. Answer :

Step 1 :

Find the intercepts.

x-intercept :

2x + 3y + 6 = 0

2x + 3(0) + 6 = 0

2x + 0 + 6 = 0

2x + 6 = 0

2x = -6

2x/2 = -6/2

x = -3

(-3, 0)

y-intercept :

2x + 3y + 6 = 0

2(0) + 3y + 6 = 0

0 + 3y + 6 = 0

3y + 6 = 0

3y = -6

3y/3 = -6/3

y = -2

(0, -2)

Step 2 :

Plot (-3, 0) and (0, -2).

Connect with a straight line.

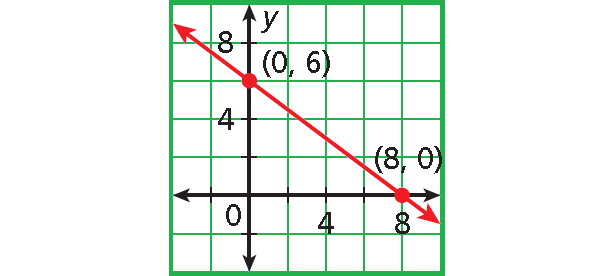
9. Answer :

Step 1 :

Find the intercepts.

x-intercept :

2y = 12 - 3x/2

2(0) = 12 - 3x/2

0 = 12 - 3x/2

12 = 3x/2

12(2/3) = (3x/2)(2/3)

8 = x

(8, 0)

y-intercept :

2y = 12 - 3x/2

2y = 12 - 3(0)/2

2y = 12 - 0/2

2y = 12 - 0

2y = 12

2y/2 = 12/2

y = 6

(0, 6)

Step 2 :

Plot (8, 0) and (0, 6).

Connect with a straight line.

10. Answer :

Neither time nor distance can be negative, so choose several nonnegative values for x. Use the function to generate ordered pairs.

f(x) = 4500 - 300x

4500

3000

1500

Graph the ordered pairs. Connect the points with a line.

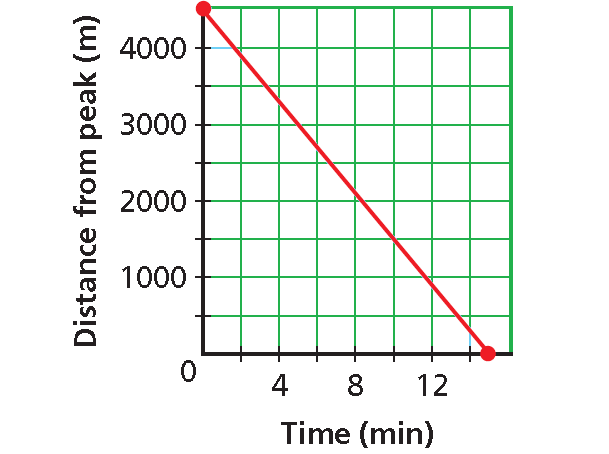
• y-intercept : 4500. This is the starting distance from the top (time = 0).

• x-intercept : 15. This the time when the tram reaches the peak (distance = 0).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

X AND Y INTERCEPTS WORKSHEET

Answers

Recent Articles

Using Partial Sums to Find Convergence or Diveregence

Digital SAT Math Problems and Solutions (part - 92)

SAT Math Resources (Videos, Concepts, Worksheets and More)