X INTERCEPTS OF A QUADRATIC FUNCTION

The graph of a quadratic function is a parabola. When a parabola opens up/down, we may have a chance to have x-intercepts.

x-intercepts are the numbers on the x-axis where a parabola intersects x-axis.

Sometimes a parabola may not intersect x-axis. In that case, there are are no x-intercepts.

Find the number of x-intercepts of the quadratic function, graph the parabola and verify it.

Example 1 :

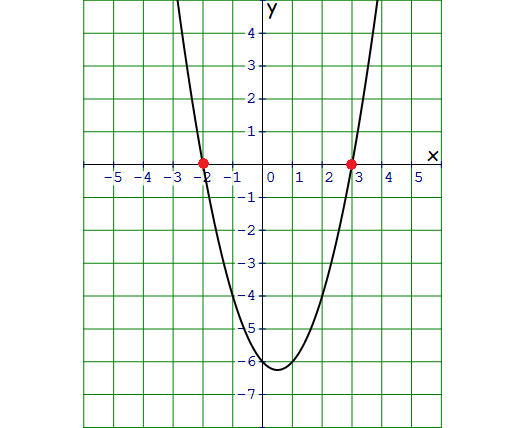
f(x) = x² - x - 6

Solution :

In the given quadratic function, put f(x) = 0.

x² - x - 6 = 0

Comparing ax² + bx + c = 0 and x² - x - 6 = 0,

a = 1, b = -1 and c = -6

Value of b² - 4ac :

= (-1)² - 4(1)(-6)

= 1 + 24

= 25 > 0

Since b² - 4ac > 0, solving the quadratic equation

x² - x - 6 = 0

will yield has two real values for x.

Then there are two x-intercepts for the given quadratic function.

Graphing :

Solve x² - x - 6 = 0 by factoring :

x² - x - 6 = 0

(x + 2)(x - 3) = 0

x + 2 = 0  or  x - 3 = 0

x = -2  or  x = 3

Two x-intercepts are -2 and 3.

Comparing f(x) = ax² + bx + c and f(x) = x² - x - 6 = 0,

a = 1, b = -1 and c = -6

a = 1 > 0 ----> parabola opens up

x-coordinate of the vertex :

x = -b/2a

Substitute a = 1 and b = -1.

x = -(-1)/2(1)

x = 1/2

x = 0.5

y-coordinate of the vertex :

Substitute x = 0.5 in f(x) = x² - x - 6.

f(0.5) = (0.5)² - (0.5) - 6

= 0.25 - 0.5 - 6

= -6.25

Vertex of the parabola is (0.5, -6.25).

Example 2 :

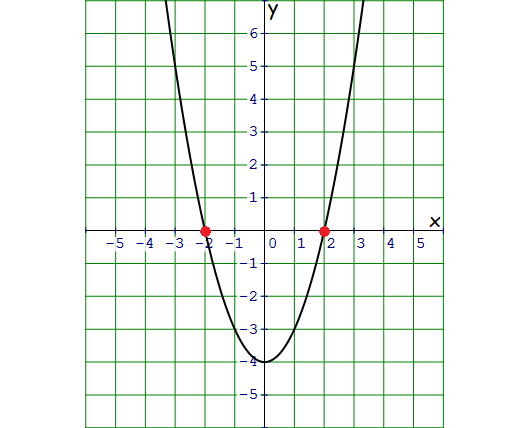
f(x) = x² - 4

Solution :

In the given quadratic function, put f(x) = 0.

x² - 4 = 0

Comparing ax² + bx + c = 0 and x² - 4 = 0,

a = 1, b = 0 and c = -4

Value of b² - 4ac :

= 0² - 4(1)(-4)

= 0 + 16

 = 16 > 0

Since b² - 4ac > 0, solving the quadratic equation

x² - 4 = 0

will yield two real values for x.

Then there are two x-intercepts for the given quadratic function.

Graphing :

Solve x² - 4 = 0 by factoring :

x² - 4 = 0

x² - 2² = 0

Using the identity a² - b² = (a + b)(a - b), 

(x + 2)(x - 2) = 0

x + 2 = 0  or  x - 2 = 0

x = -2  or  x = 2

Two x-intercepts are -2 and 2.

Comparing f(x) = ax² + bx + c and f(x) = x² - 4,

a = 1, b = 0 and c = -4

a = 1 > 0 ----> parabola opens up

x-coordinate of the vertex :

x = -b/2a

Substitute a = 1 and b = 0.

x = -(0)/2(1)

x = 0

y-coordinate of the vertex :

Substitute x = 0 in f(x) = x² - 4.

f(0) = 0² - 4

= 0 - 4

= -4

Vertex of the parabola is (0, -4).

Example 3 :

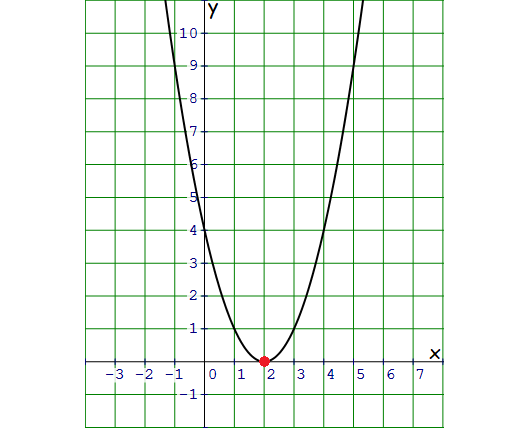
f(x) = (x - 2)²

Solution :

f(x) = (x - 2)²

Write the given quadratic function in standard form :

f(x) = (x - 2)(x - 2)

f(x) = x² - 2x - 2x + 4

f(x) = x² - 4x + 4

In the given quadratic function above, put f(x) = 0.

x² - 4x + 4 = 0

Comparing ax² + bx + c = 0 and x² - 4x + 4 = 0,

a = 1, b = -4 and c = 4

Value of b² - 4ac :

= (-4)² - 4(1)(4)

= 16 - 16

 = 0

Since b² - 4ac = 0, solving the quadratic equation

x² - 4x + 4 = 0

will yield one real value for x.

Then there is one x-intercept for the given quadratic function.

Graphing :

Solve x² - 4x + 4 = 0 by factoring :

x² - 4x + 4 = 0

(x - 2)² = 0

Taking square root on both sides,

x - 2 = 0

x = 2

x-intercept 2.

Comparing f(x) = ax² + bx + c and f(x) = x² - 4x + 4,

a = 1, b = -4 and c = 4

a = 1 > 0 ----> parabola opens up

x-coordinate of the vertex :

x = -b/2a

Substitute a = 1 and b = -4.

x = -(-4)/2(1)

x = 4/2

x = 2

y-coordinate of the vertex :

Substitute x = 2 in f(x) = x² - 4x + 4.

f(2) = 2² - 4(2) + 4

= 4 - 8 + 4

= 0

Vertex of the parabola is (2, 0).

Example 4 :

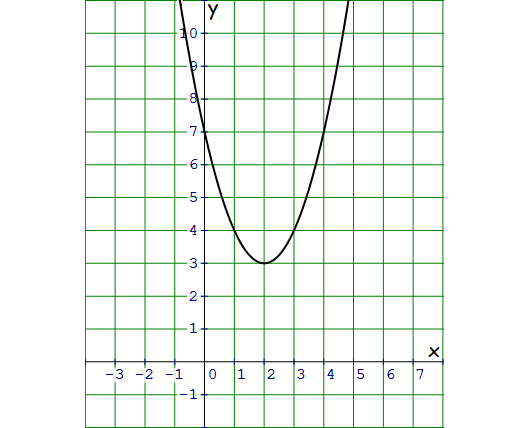
f(x) = x² - 4x + 7

Solution :

f(x) = x² - 4x + 7

In the given quadratic function above, put f(x) = 0.

x² - 4x + 7 = 0

Comparing ax² + bx + c = 0 and x² - 4x + 7 = 0,

a = 1, b = -4 and c = 7

Value of b² - 4ac :

= (-4)² - 4(1)(7)

= 16 - 28

 = -12 < 0

Since b² - 4ac < 0, solving the quadratic equation

x² - 4x + 7 = 0

will yield no real value for x.

Then there is no x-intercept for the given quadratic function.

Graphing :

Solve x² - 4x + 7 = 0 by factoring :

Already we know that b² - 4ac < 0.

So, solving x² - 4x + 7 = 0 will yield no real value for x.

There is no x-intercept. That is, the parabola will never intersect x-axis.

Comparing f(x) = ax² + bx + c and f(x) = x² - 4x + 7,

a = 1, b = -4 and c = 7

a = 1 > 0 ----> parabola opens up

x-coordinate of the vertex :

x = -b/2a

Substitute a = 1 and b = -4.

x = -(-4)/2(1)

x = 4/2

x = 2

y-coordinate of the vertex :

Substitute x = 2 in f(x) = x² - 4x + 7.

f(2) = 2² - 4(2) + 7

= 4 - 8 + 7

= 3

Vertex of the parabola is (2, 3).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.