ZEROS OF POLYNOMIAL

To find zeroes of a polynomial, we have to equate the polynomial to zero and solve for the variable.

To check whether 'k' is a zero of the polynomial f(x), we have to substitute the value 'k' for 'x' in f(x).  If f(k) = 0, then 'k' is a zero of the polynomial f(x).  

Question 1 :

Verify whether the following are zeros of the polynomial indicated against them, or not.

(i)  p(x)  =  2x - 1, x = 1/2

Solution :

p(1/2)  =  2(1/2) - 1

=  1 - 1

p(1/2)  =  0

Since we get 0 by applying 1/2, we may decide that 1/2 is the zero of the polynomial.

(ii)  p(x)  =  x³ - 1, x  =  1

Solution :

p(x)  =  x³ - 1

p(1)  =  1³ - 1

p(1)  =  0

Since we get 0 by applying 1, we may decide that 1 is the zero of the polynomial.

(iii)  p(x)  =  ax + b, x = -b/a

Solution :

p(x)  =  ax + b

p(-b/a)  =  a(-b/a) + b

p(-b/a)  =  0

Since we get 0 by applying -b/a, we may decide that -b/a is the zero of the polynomial.

(iv)  p(x)  = (x + 3) (x - 4), x = 4, x = –3

Solution :

p(x)  = (x + 3) (x - 4)

Hence 4 and -3 are the zeroes of the polynomial.

Question 2 :

Find the number of zeros of the following polynomials represented by their graphs.

(i)

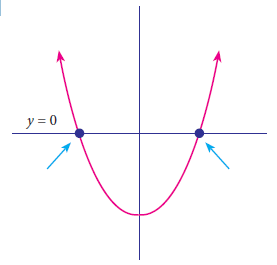
The graph intersects the x axis at two points. Hence number of zeroes is 2.

(ii)   

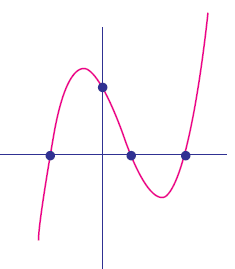
The graph intersects x-axis at 3 points, hence the number of zeroes is 3.

(iii)

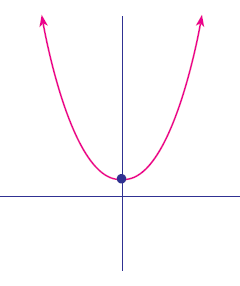
The graph does not intersect x axis. So the polynomial will not have solution.

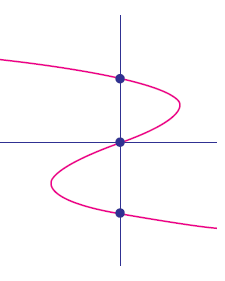
The graph intersects the x-axis at one point. Hence the polynomial will have 1 zero.

(v)

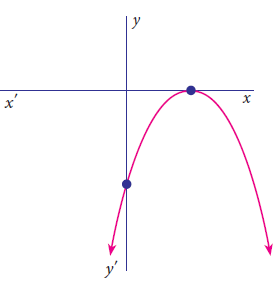
The graph intersects the x-axis at one point. Hence the polynomial will have 1 zero.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.