9th GRADE MATH WORKSHEET

Problem 1 :

Find the value of x²  + y².

Solution :

Comparing the coefficients of like terms,

x = 4  and  y = 0

The value of x² + y² :

= 4² + 0²

= 16 + 0

= 16

Problem 2 :

The dimensions of a rectangular metal sheet are 4m and 3m. The sheet is to be cut into square sheets each of side 4cm. Find the number of squares.

Solution :

Number of squares sheets :

= (400 ⋅ 300)/(4 ⋅ 4)

= 7500

Problem 3 :

Find the area of the shaded portion.

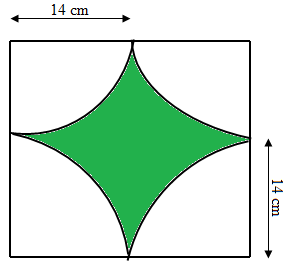
Area of shaded region 

=  Area of square - 4(Area of quadrant)

=  28² - 4(πr²/4)

=  784 - (22/7)⋅14²

=  196(4-22/7)

=  196(6/7)

=  168 cm²

Problem 4 :

Find the value of x of the following 3log ₓ5  =  1

Solution :

3logₓ5  =  1

logₓ5  =  1/3

5  =  x^1/3

Taking cubes on both sides, we get

125  =  x

So, the value of x is 125.

Problem 5 :

Out of 45 houses in a village 25 houses have Television and 30 houses have radio. Find how many of them have both.

Solution :

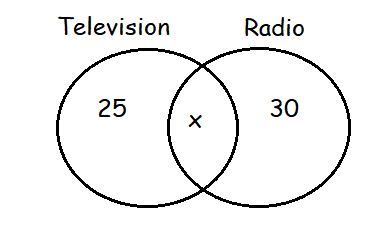
Number of students only use television  =  25-x

Number of students who use only radio  =  30-x

Let x be the number of students who use both.

Total number of students  =  45

25-x+x+30-x  =  45

55-x  =  45

x  =  55-45

x  =  10

So, the total number of students who use both is 10.

Problem 6 :

In a circle with center 0 and radius 17 cm. PQ is a chord at a distance of 8 cm from the center of the circle. Calculate the length of the chord. 

Solution :

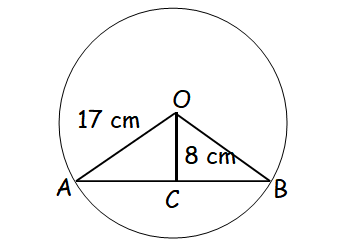
In triangle AOC,

AO²  =  AC² + OC²

17²  =  AC² + 8²

289-64  =  AC²

AC  =  225

AC  =  15

AB  =  2AC

AB  =  2(15)

AB  =  30

So, the length of chord is 30 cm.

Problem 7 :

If a + b = 2 and a² + b²  =  8, find a³ + b³

Solution :

a + b = 2  -------(1)

a² + b²  =  8  ---(2)

(a+b)² + 2ab  =  8

(a+b)² + 2ab  =  8

4+2ab  =  8

2ab  =  4

ab  =  2

a³ + b³  =  (a + b)(a²-ab+b²)

a³ + b³  =  2(8-2)

a³ + b³   =  2(6)

a³ + b³   =  12

So the value of a³ + b³ is 12.

Problem 8 :

Find the angles of x and y marked in the below given below 

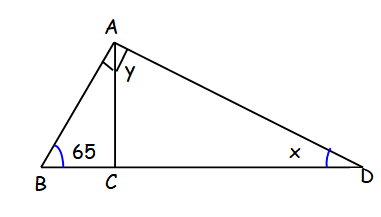
Solution :

In triangle ABD,

<ABD + <BAD + <BDA  =  180

65 + 90 + x  =  180

155+x  =  180

x  =  180-155

x  =  25

In triangle ACD,

<ACD + <CDA + <DAC  =  180

90 + 25 + y  =  180

y  =  180 - 115

y  =  65

Problem 9 :

The sum of two numbers is 25 and their difference is 13. Find their product.

Solution :

Let x and y be two numbers.

x + y  =  25  -----(1)

x - y  =  13  -----(2)

(1) + (2)

2x  =  38

x  =  19

By applying the value of x in (1), we get

19 + y  =  25

y  =  25 - 19

y  =  6

Product of two numbers  =  19(6)

=  114

So, the product of two numbers is 114.

Problem 10 :

The sum of the digits of a two digit number is 10. If the number formed by reversing the digits is less than the original number by 36, find the required number.

Solution :

Let xy be the two digit number

x + y  =  10 ----(1)

yx  =  xy - 36

10y - x  =  10x + y - 36

9x - 9x  =  36

x - y  =  4 ----(2)

(1) + (2)

2x  =  14

x  =  7

By applying the value of x in (1), we get

7 + y  =  10

y  =  3

So, the required number is 73.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.