GCD OF POLYNOMIALS USING DIVISION ALGORITHM

If f (x) and g(x) are two polynomials of same degree then the polynomial carrying the highest coefficient will be the dividend.

In case, if both have the same coefficient then compare the next least degree’s coefficient and proceed with the division.

If r (x) = 0 when f(x) is divided by g(x) then g(x) is called GCD of the polynomials.

Example 1 : 

Find the GCD of the following polynomials.

x⁴ + 3x³ −x −3, x³ +x² −5x + 3

Solution :

Let f(x)  =  x⁴ + 3x³ −x −3

g(x)  =  x³ +x² −5x + 3

The degree of the polynomial f(x) is greater than g(x).

Note : If we have any missing term, we have to replace that place by 0.

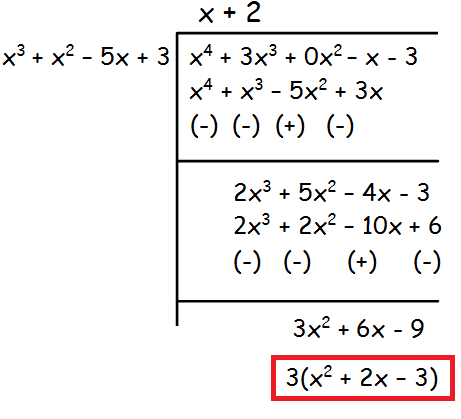
The remainder is 3(x² + 2x - 3), which is not equal to 0.So, we have to divide x³ +x² −5x + 3 by x² + 2x - 3 by leaving the remainder.

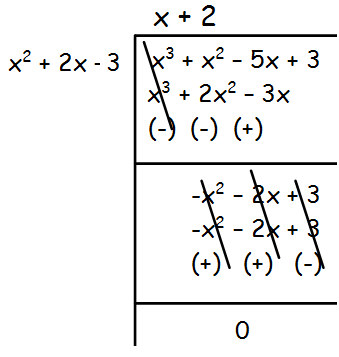
We get 0 as remainder by dividing the given polynomial by x² + 2x - 3.

Hence the required GCD is x² + 2x - 3.

Example 2 : 

Find the GCD of the following polynomials.

x⁴  - 1,  x³ - 11x² + x - 11

Solution :

Let f(x)  =  x⁴  - 1

g(x)  =  x³ - 11x² + x - 11

The degree of the polynomial f(x) is greater than g(x).

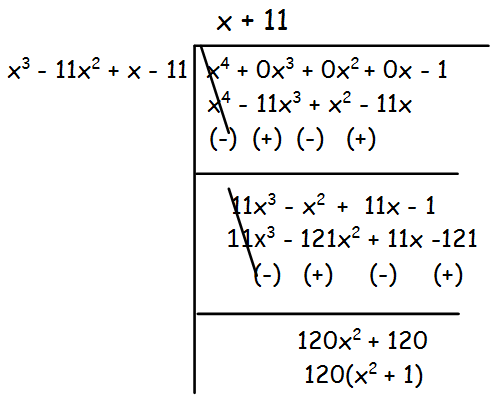
The remainder is 120(x² + 1), which is not equal to 0.So, we have to divide  x³ - 11x² + x - 11 by 120(x² + 1) by leaving the remainder.

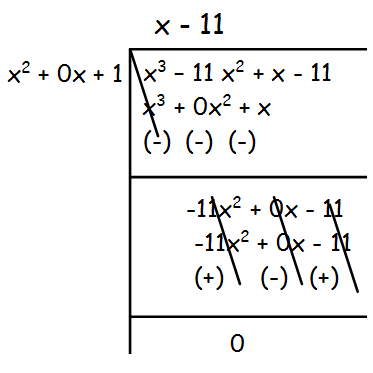
Hence the G.C.D is x² + 1

Example 3 : 

Find the GCD of the following polynomials.

3x⁴ + 6x³ −12x² −24x, 4x⁴ +14x³ + 8x² −8x

Solution :

Let f(x)  =  3x⁴ + 6x³ −12x² −24x

f(x)  =  3x(x³ + 2x² - 4x - 8)

g(x)  =  4x⁴ +14x³ + 8x² −8x

 g(x)  =  2x (x³ + 7x² + 4x - 4) 

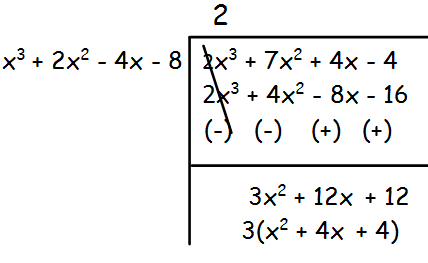
The remainder is 3(x² + 4x + 4), which is not equal to 0.So, we have to divide  x³ + 2x² - 4x - 8 by x² + 4x + 4 by leaving the remainder.

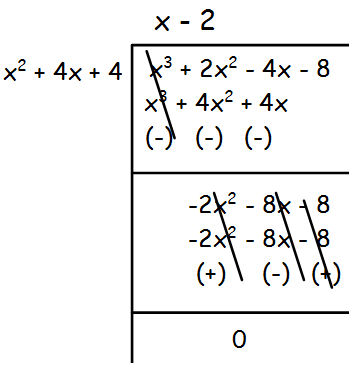
By dividing x² + 4x + 4, we get 0 remainder. The term x is also common for both the polynomials.

Hence the G.C.D is x(x² + 4x + 4).

Example 4 : 

Find the GCD of the following polynomials.

3x³ + 3x² + 3x + 3 , 6x³ +12x² + 6x +12

Solution :

Let f(x)  =  3x³ + 3x² + 3x + 3

f(x)  =  3(x³ + x² + x + 1)

g(x)  =  6x³ + 12x² + 6x + 12

g(x)  =  6(x³ + 2x² + x + 2)

The remainder is (x² + 0x + 1), which is not equal to 0.So, we have to divide  x³ + x² + x + 1 by x² + 0x + 1 by leaving the remainder.

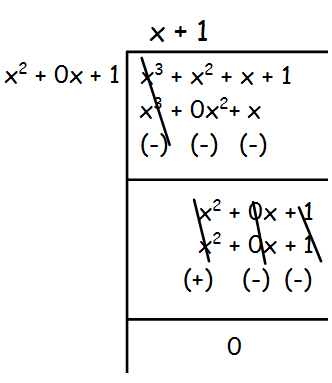
By dividing x² + 1, we get 0 remainder. The constant 3 is also common for both the polynomials.

Hence the G.C.D is 3(x² + 1).

Example 5 :

Find the HCF and LCM of the expressions x² - 5x + 6 and x² - 7x + 10 by factorization.

Solution :

x² - 5x + 6 =  x² - 2x - 3x + 6

= x(x - 2) - 3(x - 2)

= (x - 2)(x - 3) -----(1)

x² - 7x + 10 = x² - 5x - 2x + 10

= x(x - 5) - 2(x - 5)

= (x - 2)(x - 5) -------(2)

Comparing (1) and (2)

HCF = x - 2

LCM = (x - 2)(x - 3)(x - 5)

Example 6 :

Find the HCF and LCM of the expressions (x + 3) (6x² + 5x - 4) and (2x² + 7x + 3)(x + 3) by factorization.

Solution :

(x + 3) (6x² + 5x - 4)

= (x + 3) (6x² + 8x - 3x - 4)

= (x + 3) [2x(3x + 4) - 1(3x + 4)]

= (x + 3) (2x - 1)(3x + 4) -------(1)

(2x² + 7x + 3)(x + 3)

= (2x² + 6x + 1x + 3)(x + 3)

= [2x(x + 3) + 1(x + 3)](x + 3)

= (2x + 1)(x + 3)(x + 3)

= (2x + 1)(x + 3)² -------(2)

Comparing (1) and (2)

LCM = (x + 3)² (2x - 1)(3x + 4)(2x + 1)

HCF = x + 3

Example 7 :

Find the HCF and LCM of the expressions 

(x² + xy + y²) and (x³ - y³)

Solution :

(x² + xy + y²) and (x³ - y³)

= (x² + xy + y²) ------(1)

The first expression cannot factorable.

x³ - y³ = (x - y)(x² + xy + y²) ------(2)

Comparing (1) and (2)

LCM = (x² + xy + y²) (x - y)

HCF = (x² + xy + y²)

Example 8 :

Find the HCF and LCM of the expressions 

(x² - 9) and (x² - 6x + 9)

Solution :

(x² - 9) = x² - 3²

= (x - 3)(x + 3) ------(1)

x² - 6x + 9 = x² - 3x - 3x + 9

= [x(x - 3) - 3(x - 3)]

= (x - 3)(x - 3)

= (x - 3)² ------(2)

Comparing (1) and (2)

LCM = (x - 3)² (x + 3)

HCF = (x - 3)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.