SOLVING ABSOLUTE VALUE EQUATIONS AND INEQUALITIES

Solving Absolute Value Equations

The general form of an absolute value equation is

|ax + b| = k

In the above absolute value equation, we can notice that there is only absolute part on the left side.

(Here "a" and "k" are real numbers)

Let us consider the absolute value equation |2x + 3| = 5.

We can solve the absolute value equation |2x + 3| = 5 as shown below.

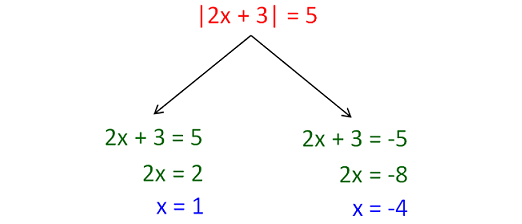
The following steps will be useful to solve absolute value equations.

Step 1 :

Get rid of absolute sign and divide it into two branches. 

Step 2 :

For the first branch, take the sign as it is on the right side.  

Step 3 :

For the second branch, change the sign on the right side.

Step 4 :

Then solve both the branches. 

Solving Absolute Value Inequalities

The general form of an absolute value inequality is

|ax + b| ≤ k

or

|ax + b| ≥ k

Method 1 : (Less Than or Equal to)

Solve the absolute value inequality given below

|x + 2| ≤ 3

Solution :

We can solve the absolute value inequality |x + 2| ≤ 3 as shown below. 

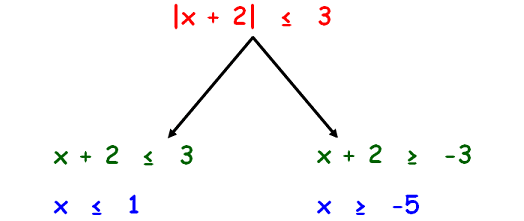
Let us graph the solution of the first branch  x ≤ 1.

Let us graph the solution of the second branch  x ≥ -5.

If we combine the above two graphs, we will get a graph as shown below below. 

From the above graph, the solution for |x + 2| ≤ 3 is

-5 ≤ x ≤ 1

Method 2 : (Greater Than or Equal to)

Solve the absolute value inequality given below

|x - 3| ≥ 1

Solution :

We can solve the absolute value inequality |x - 3| ≥ 1 as shown below. 

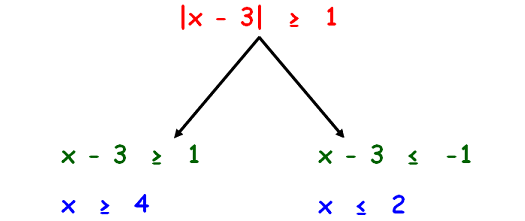
Let us graph the solution of the first branch  x ≥ 4.

Let us graph the solution of the second branch  x ≤ 2.

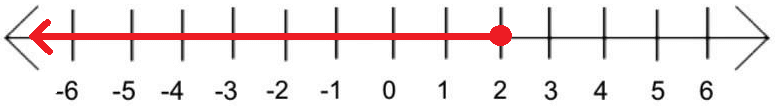
If we combine the above two graphs, we will get a graph as shown below below. 

From the above graph, the solution for |x - 3| ≥ 1 is

(-∞, 2] U [3, +∞)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.