ADD AND SUBTRACT POLYNOMIALS

Adding polynomials and subtracting polynomials is nothing but combining the like terms.

Let us consider the following problem. 

Add : (3x³-5x²+ 2x-7) and (4x²+x-8)

Here we give step by step explanation for adding the above two polynomials.

Step 1 :

Before going to add two polynomials, first we have to arrange the given polynomials one by one from highest power to lowest power.

(3x³-5x²+ 2x-7) and (4x²+x-8)

The two given polynomials are already in the arranged form.So we can leave it as it is.

Step 2 :

Now we have to write the like terms together starting from the highest power to lowest power.

     = (3x³-5x²+ 2x-7) + (4x²+ x - 8)

Step 3:

Combine the like terms (Add or subtract) based on the signs of those terms.

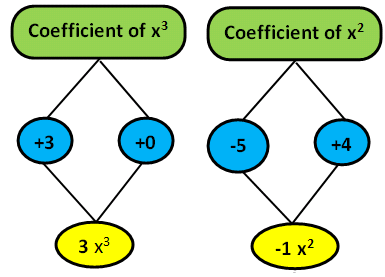
In the second polynomial,we do not have x³ term,so we have to consider that there is zero x³. 

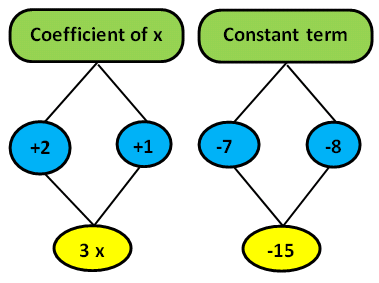
So the final answer is  3x³ - 1x² + 3x - 15

Example :

Add ( 7p³ +  4p²- 8p + 1 ) and (3p³- 5p²- 10p + 5)

Solution : 

Step 1:

The two given polynomials are already in the arranged form.So we can leave it as it is.

          =  ( 7p³ + 4p²- 8p + 1) + (3p³ - 5p² - 10p + 5)

Step 2 :

Now we have to write the like terms together starting from the highest power to lowest power.

          = 7p³ + 3p³ + 4p²- 5p²- 8p - 10p + 1 + 5

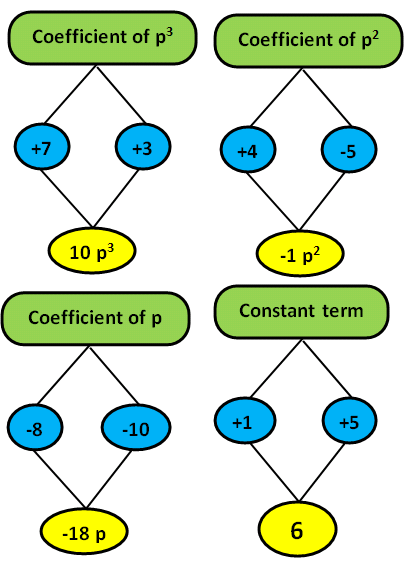
So the final answer is  10p³- 1p²- 18p + 6

Subtracting polynomials

Example  :

Subtract the following polynomials:

(2 x³ - 2 x² + 4 x - 3)- (x³ + x² - 5 x + 4)

Solution :

Step 1:

In the first step we are going to multiply the negative with inner terms.

                    = 2 x³ -2 x² + 4 x - 3 - x³-x²+ 5 x - 4 

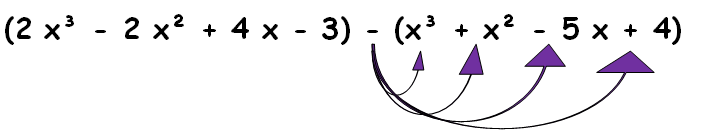
Step 2:

In the second step we have to combine the like terms 

                   = 2 x³ - x³ - 2 x²- x² + 4 x + 5 x - 3 - 4

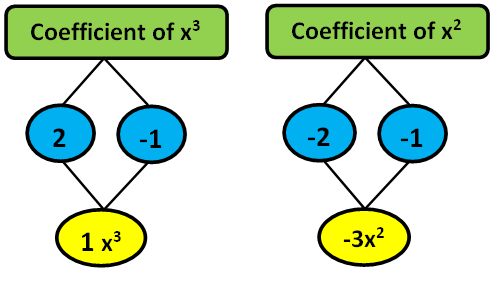
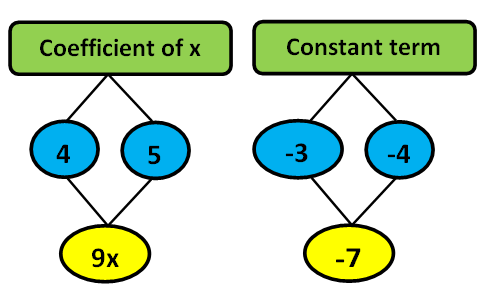
Step 3:

After combining the like terms we will get the answer

                  = x³ - 3 x² + 9x - 7

Adding and subtracting polynomials sample problems

Problem 1 :

Add ( 2x³ + 5x² - 2x + 7 ) and ( x³ + 4x² - x + 6)

Solution : 

=  ( 2x³ + 5x² - 2x + 7 ) + ( x³ + 4x² - x + 6)

=  2x³ + 5x² - 2x + 7 + x³ + 4x² - x + 6

=  2x³ + x³ + 5x² + 4x² - 2x - x + 7 + 6

=  3x³ + 9x² - 3x + 13

Problem 2 :

Add ( 3x³ - 2x² - x + 4 ) and ( 2x³ + 7x² - 3x - 3 )

Solution : 

    =  (3x³ - 2x² - x + 4) + (2x³ + 7x² - 3x - 3)

    =  3 x³ - 2 x² - x + 4 + 2 x³ + 7 x² - 3 x - 3

    =  3x³ + 2x³ - 2x² + 7x² - x - 3x + 4 - 3

    =  5x³ + 5x² - 4x + 1   

Problem 3 :

Add  2( x³ - x² + 6x - 2 ) and ( 5x⁶ + 7x⁵ - 3x - 3 )

Solution : 

    =  2( x³ - x² + 6 x - 2 ) + ( 5 x⁶ + 7 x⁵ - 3 x - 3 )

    =  2x³ - 2x² + 12x - 4 + 5x⁶ + 7x⁵ - 3x - 3

    =  5x⁶ + 7x⁵ + 2x³ - 2x² + 12x - 3x - 4 - 3

    =  5x⁶ + 7x⁵ + 2x³ - 2x² + 9x - 7

Problem 4 :

Add -1( x⁶ + x³ + 6x² - 2 ) and 2( 5x⁶ + 7x⁵ - 3x - 3 )

Solution : 

    =  -1( x⁶ + x³ + 6x² - 2 ) + 2( 5x⁶ + 7x⁵ - 3x - 3 )

    =  -x⁶ - x³ - 6x² + 2 + 10x⁶ + 14x⁵ - 6x - 6

    =  -x⁶ + 10x⁶ + 14x⁵ - x³ - 6x² - 6x + 2 - 6

    =  9x⁶ + 14x⁵ - x³ - 6x² - 6x - 4

Problem 5 :

Add 5( 5x⁶ + 2x³ - 6x² - 2 ) + 6(-3x⁶ + 2x⁵ + 2x + 1 )

Solution : 

    =  5( 5x⁶ + 2x³ - 6x² - 2 ) + 6( -3x⁶ + 2x⁵ + 2x + 1 )

    =  25x⁶ + 10x³ - 30x² - 10 -18x⁶ + 12x⁵ + 12x + 6

    =  25x⁶ -18x⁶ + 12x⁵ + 10x³ - 30x² + 12x -10 + 6

    =  7x⁶ + 12x⁵ + 10x³ - 30x² + 12x - 4

Example problems of subtracting polynomials

Question 1 :

Subtract 2x³ + 5x² - 2x - 11 from 3x³ - 2x² - 5x - 6

Solution :

= ( 3x³ - 2x² - 5x - 6 ) - ( 2x³ + 5x² - 2x - 11 )

   = 3x³ - 2x² - 5x - 6 -2x³ - 5x² + 2x + 11

   = 3x³ - 2x³ - 2x² - 5x² - 5x + 2x - 6 + 11

   = x³ - 7x² - 3x + 5

Question 2 :

Subtract x³ + 4x² - 12x - 5  from 5x³ + 3x² + 2x - 10

Solution : 

 = ( 5x³ + 3x² + 2x - 10 ) - ( x³ + 4x² - 12x - 5 )

   = 5x³ + 3x² + 2x - 10 - x³ - 4x² + 12x + 5 

   = 5x³ - x³ + 3x² - 4x² + 2x + 12x - 10 + 5 

   = 4x³ - x² + 14x - 5

Question 3 :

Subtract 12x³ + 14x² + 17x - 12 from 15x³+22x²+17x-19 

Solution :

= ( 15x³ + 22x² + 17x - 19 ) - ( 12x³ + 14x² + 17x - 12 )

   = 15x³ + 22x² + 17x - 19 - 12x³ - 14x² - 17x + 12

   = 15x³ - 12x³ + 22x² - 14x² + 17x - 17x - 19 + 12

   = 3x³ + 8x² + 0x - 7

   = 3x³ + 8x² - 7

Question 4 :

Subtract 5x³ + 3x² + 7x - 6 from 3x³ + 2x² + 6x - 4

Solution :

 = ( 3x³ + 2x² + 6x - 4 ) - ( 5x³ + 3x² + 7x - 6 )

   = 3x³ + 2x² + 6x - 4 - 5x³ - 3x² - 7x + 6

   = 3x³ - 5x³ + 2x² - 3x² + 6x - 7x - 4 + 6

   = -2x³ - x² - x + 2

Question 5 :

Subtract x³ + 32x² + 17x - 16 from 13x³+23x²+16x-14

Solution :

 = ( 13x³ + 23x² + 16x - 14 ) - ( x³ + 32x² + 17x - 16 )

   = 13x³ + 23x² + 16x - 14 - x³ - 32x² - 17x + 16

   = 13x³ - x³ + 23x² - 32x² + 16x - 17x - 14 + 16

   = 12x³ - 9x² - x + 2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.