AMPLITUDE PERIOD PHASE SHIFT AND VERTICAL SHIFT OF SINUSOID FUNCTION

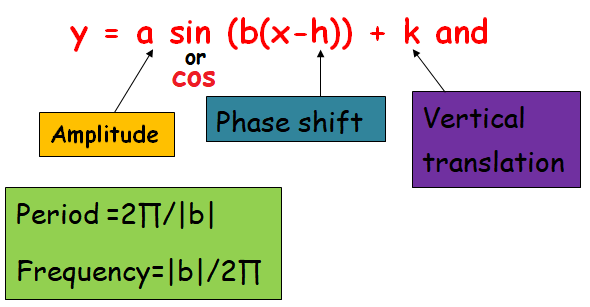
A function is a sinusoid if it can be written in the form

f (x)  =  a sin (bx+c)+d

where a, b, c, and d are constants and neither a nor b is 0.

Example 1 :

State the amplitude and period of the sinusoid, and (relative to the basic function) the phase shift and vertical translation

y  =  -2 sin (x - π/4) + 1

Solution :

Amplitude  =  2

Period  =  2π/|b|  ==>  2π/|1|  ==>  2π

Frequency  =  1/2π

Phase shift  =  π/4 (π/4 units to the right)

Vertical shift  =  1 (Move one unit to up)

In front of the given function, we have negative. So we should do reflection.

So, every sin curve will fit into the interval 0 to 2π.

Example 2 :

Graph the following function

y  =  5 cos (3x - π/6) + 0.5

Solution :

Amplitude  =  5

Period  =  2π/|b|  ==>  2π/|3|  ==>  2π/3

Frequency  =  3/2π

Phase shift  =  π/6 (π/6 units to the right)

Vertical shift  =  0.5 (Move 0.5 unit to up)

So, every cosine curve will fit into the interval 0 to 2π/3.

Example 3 :

Graph the following function

y  =  -3.5 sin (2x - π/2) - 1

Solution :

Amplitude  =  3.5

Period  =  2π/|b|  ==>  2π/|2|  ==>  π

Frequency  =  1/π

Phase shift  =  π/2 (π/2 units to the right)

Vertical shift  =  1 (Move 1 unit to down)

So, every sin curve will fit into the interval 0 to π.

Example 4 :

Graph the following function

y  =  3 cos (x + 3) - 2

Solution :

Amplitude  =  3

Period  =  2π/|b|  ==>  2π/|1|  ==>  2π

Frequency  =  1/2π

Phase shift  =  3 (3 units to the left)

Vertical shift  =  2 (Move 2 units to down)

So, every cosine curve will fit into the interval 0 to 2π.

Example 5 :

Graph the following function

y  =  7/3 sin (x + 5/2) - 1

Solution :

Amplitude  =  7/3

Period  =  2π/|b|  ==>  2π/|1|  ==>  2π

Frequency  =  1/2π

Phase shift  =  5/2 (2.5 units to the left)

Vertical shift  =  1 (Move 1 unit to down)

So, every sin curve will fit into the interval 0 to 2π.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.