ANGLE BISECTOR THEOREM WORKSHEET

1. In the ΔABC shown below, find the length of BD.

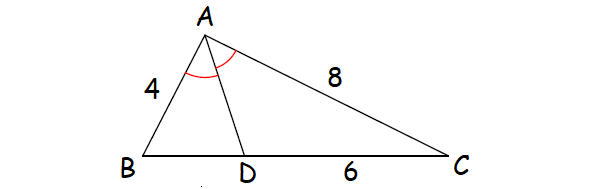
2. In the ΔABC shown below, find the length of CD.

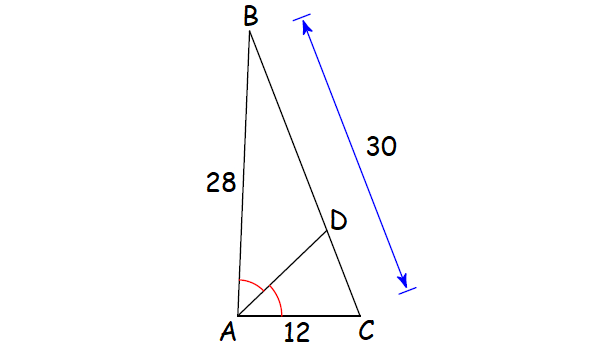
3. Solve for x.

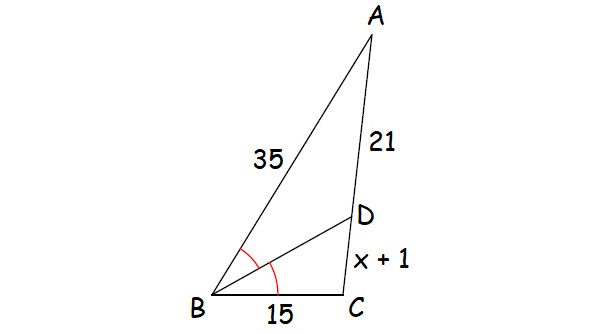
4. Solve for x.

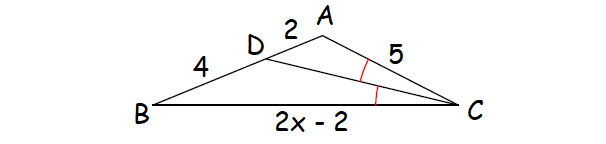
5. Solve for x.

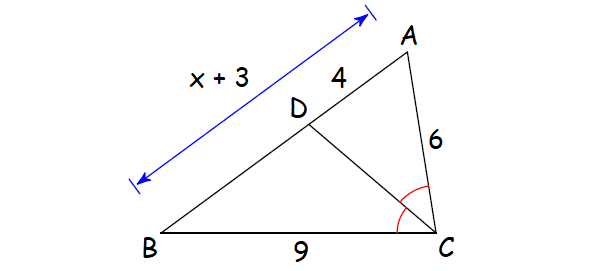
6. Solve for x.

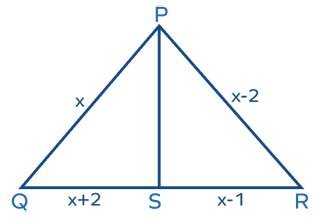
7.  In triangle PQR as shown below, PS is the angle bisector of <P. Find the lengths of sides of triangle PQR.

8. Which of the following options represent the statement of angle bisector theorem for the given triangle ?

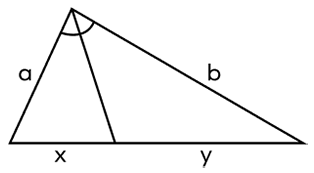
a)  a/x = y/b     b)  a/x = 2b/y    c) a/b = x/y   d) none

9. The __________ of a triangle divides the opposite sides in the ratio equal to the ratio of the remaining two sides.

a)  angle bisector    b)  median

c)  Perpendicular bisector       d)  height

10.  In the figure, CP is an altitude, CQ is the angle bisector of <ACB, and R is the midpoint of AB.

a)  Find ∠ACQ if ∠ACB = 123 - x and ∠QCB = 42 + x

b)  Find AB if AR = 3x + 6 and RB = 5x - 14

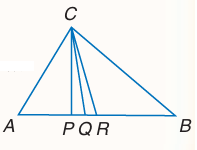
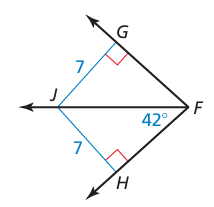
11. Find each measure 

a)  ∠GFJ

b) RS

1. Answer :

Since AD is the angle bisector of ∠A, by Angle Bisector Theorem,

BD/DC = AB/AC

Substitute.

BD/6 = 4/8

BD/6 = 1/2

Multiply each side by 6.

BD = 3

2. Answer :

Let x be the length of CD.

Then the length of DB = 30 - x.

Since AD is the angle bisector of ∠A, by Angle Bisector Theorem,

CD/DB = AC/AB

Substitute.

x/(30 - x) = 12/28

x/(30 - x) = 3/7

7x = 3(30 - x)

7x = 90 - 3x

Add 3x to each side.

10x = 90

Divide each side by 10.

x = 9

CD = 9

3. Answer :

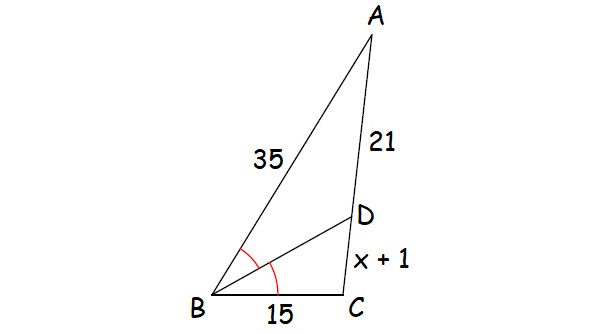
Since BD is the angle bisector of ∠B, by Angle Bisector Theorem,

CD/DA = BC/BA

Substitute.

(x + 1)/21 = 15/35

(x + 1)/21 = 3/7

7(x + 1) = 3(21)

7x + 7 = 63

Subtract 7 from each side.

7x = 56

Divide each side by 7.

x = 8

4. Answer :

Since CD is the angle bisector of ∠C, by Angle Bisector Theorem,

AD/DB = CA/CB

Substitute.

2/4 = 5/(2x - 2)

1/2 = 5/(2x - 2)

1(2x - 2) = 5(2)

2x - 2 = 10

Add 2 to each side.

2x = 12

Divide each side by 2.

x = 6

5. Answer :

Find the length of DB :

DB = AB - AD

= (x + 3) - 4

= x + 3 - 4

= x - 1

Since CD is the angle bisector of ∠C, by Angle Bisector Theorem,

AD/DB = CA/CB

Substitute.

4/(x - 1) = 6/9

4/(x - 1) = 2/3

3(4) = 2(x - 1)

12 = 2x - 2

Add 2 to each side.

14 = 2x

Divide each side by 2.

7 = x

6. Answer :

Find the length of AD :

AD = AC - DC

= 18 - 8

= 10

Since BD is the angle bisector of ∠B, by Angle Bisector Theorem,

CD/DA = BC/BA

Substitute.

8/10 = (2x - 4)/15

4/5 = (2x - 4)/15

15(4) = 5(2x - 4)

60 = 10x - 20

Add 20 to each side of the equation.

80 = 10x

Divide each side by 10.

8 = x

7. Answer :

Using angle bisector theorem,

PQ/PR = QS/SR

x/(x - 2) = (x + 2)/(x - 1)

Doing cross multiplication, we get

x(x - 1) = (x + 2)(x - 2)

x² - x = x² - 4

-x = -4

x = 4

PQ = x ==> 4 cm

PR = x - 2 ==> 4 - 2 ==> 2 cm

QS = x + 2 ==> 4 + 2 ==> 6 cm

SR = x - 1 ==> 4 - 1 ==> 3 cm

8. Answer :

a/b = x/y

So, option c is correct.

9. Answer :

The angle bisector of a triangle divides the opposite sides in the ratio equal to the ratio of the remaining two sides.

10. Answer :

a)  In the figure, CP is an altitude, CQ is the angle bisector of <ACB, and R is the midpoint of AB.

Find ∠ACQ if ∠ACB = 123 - x and ∠QCB = 42 + x

∠ACQ + ∠QCB = ∠ACB

∠ACQ = ∠ACB - ∠QCB

= 123 - x - (42 + x)

= 123 - x - 42 - x

∠ACQ = 81 - 2x

b)  Since R is the midpoint 

AR = RB

3x + 6 = 5x - 14

3x - 5x = -14 - 6

-2x = -20

x = 20/2

x = 10

Applying the value of x in the measure of ∠ACQ

= 81 - 2(10)

= 81 - 20

∠ACQ = 61

11. Answer :

∠GFJ = ∠HFJ = 42 degree

PS = RS

5x = 6x - 5

5x - 6x = -5

-x = -5

x = 5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.