ANGLE PAIR RELATIONSHIPS

Relationship 1 :

Two angles are vertical angles, if their sides form two pairs of opposite rays.

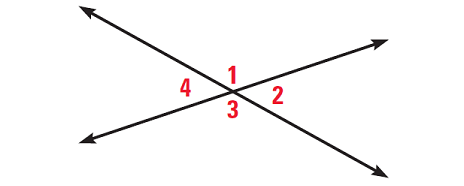
m∠1 and m∠3 are vertical angles

m∠2 and m∠4 are vertical angles

Relationship 2 :

Two adjacent angles are a linear pair, if their non-common sides are opposite rays.

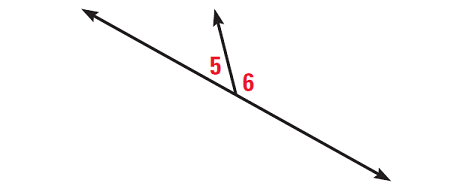
m∠5 and m∠6 are a linear pair. 

Example 1 :

Look at the picture shown below and answer the following questions.

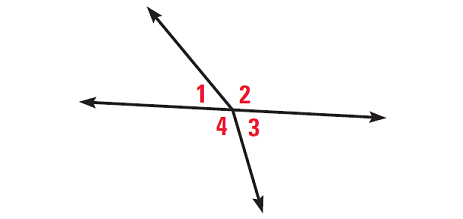
(i) Are m∠2 and m∠3 a linear pair?

(ii) Are m∠3 and m∠4 a linear pair?

(iii) Are m∠1 and m∠3 vertical angles?

(iv) Are m∠2 and m∠4 vertical angles?

Solution :

Solution (i) :

No. The angles are adjacent but their non-common sides are not opposite rays.

Solution (ii) :

Yes. The angles are adjacent and their non-common sides are opposite rays.

Solution (iii) :

No. The sides of the angles do not form two pairs of opposite rays.

Solution (iv) :

No. The sides of the angles do not form two pairs of opposite rays.

Example 2 :

In the stair railing shown at the right,  m∠6 has a measure of 130°. Find the measures of the other three angles.

Solution :

m∠6 and m∠7 are a linear pair. So, the sum of their measures is 180°.

m∠6 + m∠7 = 180°

Substitute m∠6 = 130°.

130° + m∠7 = 180°

Subtract 130° from both sides.

m∠7 = 50°

m∠6 and m∠5 are also a linear pair. So, it follows that m∠7 = 50°.

m∠6 and m∠8 are vertical angles. So, they are congruent and they have same measure.

m∠8 = m∠6 = 130°

Example 3 :

In the diagram shown below, Solve for x and y. Then, find the angle measures.

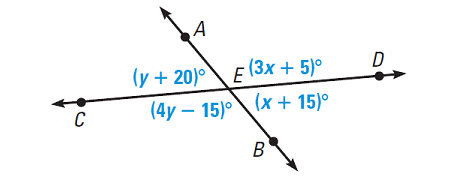
Solution :

Use the fact that the sum of the measures of angles that form a linear pair is 180°.

Solving for x :

m∠AED and m∠DEB are a linear pair. So, the sum of their measures is 180°.

m∠AED + m∠DEB = 180°

Substitute m∠AED = (3x + 5)° and m∠DEB = (x + 15)°.

(3x + 5)° + (x + 15)° = 180°

Simplify.

4x + 20 = 180

Subtract 20 from both sides.

4x = 160

Divide both sides by 4.

x = 40

Solving for y :

m∠AEC and m∠CEB are a linear pair. So, the sum of their measures is 180°.

m∠AEC + m∠CEB = 180°

Substitute m∠AEC = (y + 20)° and m∠CEB = (4y - 15)°.

(y + 20)° + (4y - 15)° = 180°

Simplify.

5y + 5 = 180

Subtract 5 from both sides.

5y = 175

Divide both sides by 5.

y = 35

Use substitution to find the angle measures :

m∠AED = (3x + 5)°

= (3 • 40 + 5)°

= 125°

m∠DEB = (x + 15)°

= (40 + 15)°

= 55°

m∠AEC = ( y + 20)°

  = (35 + 20)°

= 55°

m∠CEB = (4y - 15)°

= (4 • 35 - 15)°

= 125°

So, the angle measures are 125°, 55°, 55°, and 125°. Because the vertical angles are congruent, the result is reasonable.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.