ANGLES AND PARALLEL LINES

When two parallel lines are cut by a transversal, the following pairs of angles are congruent.

• corresponding angles

• alternate interior angles

• alternate exterior angles

• consecutive interior angles are supplementary

Example 1 :

In the figure shown below, m∠2 = 75°. Find the measures of the remaining angles.

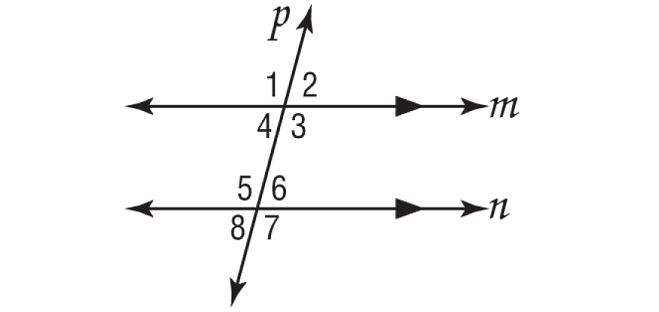
Solution :

∠1 and ∠2 form a linear pair and they are supplementary.

m∠1 + m∠2 = 180°

m∠1 + 75° = 180°

m∠1 = 105°

∠1 and ∠3 are vertical angles and they are equal.

m∠3 = m∠1

m∠3 = 105°

∠2 and ∠4 are vertical angles and they are equal.

m∠4 = m∠2

m∠4 = 75°

∠1 and ∠5 are corresponding angles and they are equal.

m∠5 = m∠1

m∠5 = 105°

∠2 and ∠6 are corresponding angles and they are equal.

m∠6 = m∠2

m∠6 = 75°

∠4 and ∠8 are corresponding angles and they are equal.

m∠8 = m∠4

m∠8 = 75°

∠3 and ∠7 are corresponding angles and they are equal.

m∠7 = m∠3

m∠7 = 105°

Example 2 :

In the figure shown below, m∠3 = 102°. Find the measure of each angle. Tell which postulate(s) or theorem(s) you used.

a. ∠5       b. ∠6       c. ∠11       d. ∠7       e. ∠15       f. ∠14

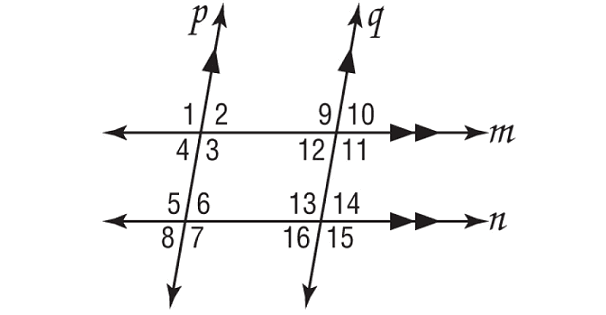
Solution :

(a) :

m∠5 = m∠3

m∠5 = 102°

(Alternate Interior Angles Theorem)

(b) : 

m∠3 + m∠6 = 180°

102° + m∠6 = 180°

m∠6 = 78°

(Interior Angles on the Same Side of the Transversal Theorem)

(c) :

m∠11 = m∠3

m∠11 = 102°

(Corresponding Angles Postulate)

(d) :

m∠7 = m∠3

m∠7 = 102°

(Corresponding Angles Postulate)

(e) :

m∠15 = m∠7

m∠15 = 102°

(Corresponding Angles Postulate)

(f) :

m∠14 = m∠6

m∠14 = 78°

(Corresponding Angles Postulate)

Example 3 :

In the figure shown below, m∠5 = 68° and m∠9 = 80°. Find the measure of each angle. Tell which postulate(s) or theorem(s) you used.

a. ∠12       b. ∠1       c. ∠4       d. ∠3       e. ∠7       f. ∠16

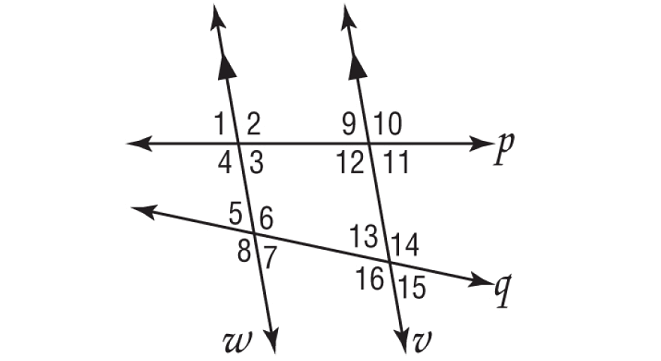
Solution :

(a) :

m∠9 + m∠12 = 180°

80° + m∠12 = 180°

m∠12 = 100°

(Linear Pair Postulate)

(b) :

m∠1 = m∠9

m∠1 = 80°

(Corresponding Angles Postulate)

(c) :

m∠4 = m∠12

m∠4 = 100°

(Corresponding Angles Postulate)

(d) :

m∠3 = m∠9

m∠3 = 80°

(Alternate Interior Angles Theorem)

(e) :

m∠7 = m∠5

m∠7 = 68°

(Vertical Angles Theorem)

(f) :

m∠7 + m∠16 = 180°

68° + m∠16 = 180°

m∠16 = 112°

(Interior Angles on the Same Side of the Transversal Theorem)

Algebra and Angle Measures

Algebra can be used to find unknown values in angles formed by a transversal and parallel lines.

Example 4 :

If m∠1 = 3x + 15, m∠2 = 4x - 5, and m∠3 = 5y, find the value of x and y.

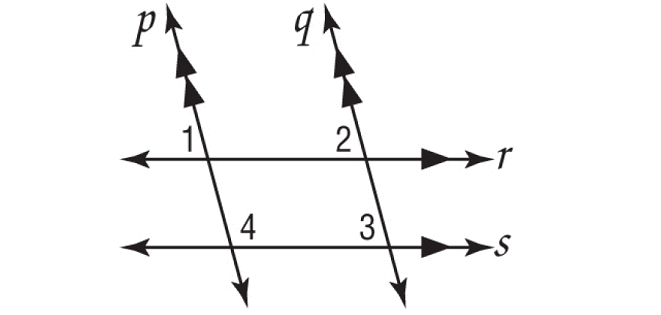
Solution :

∠1 and ∠2 are corresponding angles and they are equal.

m∠1 = m∠2

3x + 15 = 4x - 5

Subtract 3x from each side.

15 = x - 5

Add 5 to each side.

20 = x

∠2 and ∠3 are corresponding angles and they are equal.

m∠2 = m∠3

4x - 5 = 5y

Substitute x = 20.

4(20) - 5 = 5y

80 - 5 = 5y

75 = 5y

Divide each side by 5.

15 = y

Therefore,

x = 20 and y = 15

Using Auxiliary Lines

Example 5 :

Using a 3^rd parallel Line – Auxiliary Line, find the value of x.

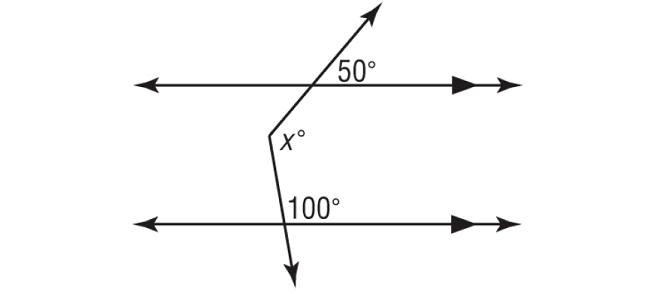
Solution :

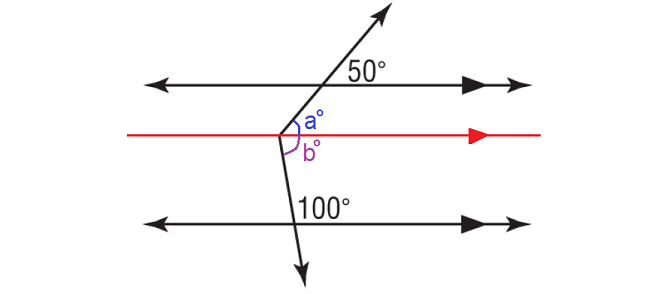
In the figure above, a° and 50° are corresponding angles and they are equal.

a° = 50°

b° and 100° are interior angles on the same side of the transversal and they are supplementary.

b° + 100° = 180°

Subtract 100° from each side.

b° = 80°

In the figure above,

x = a + b

= 50 + 80

= 130

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.