ANSWERS FOR MATH QUESTIONS

Question 1 :

Draw the net of this figure. Label Your diagram.

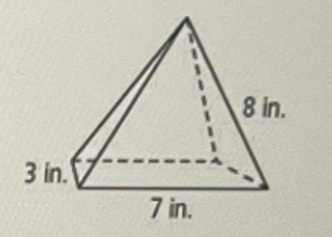
Answer :

Plot the vertices of the given pyramid with alphabets A,B, C, D and E as shown below.

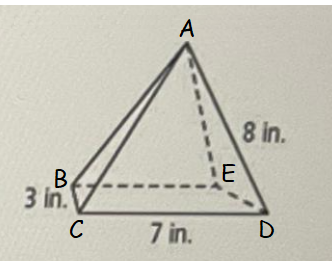
Imagine the above pyramid is made up of piece of papers. It has four walls. When all the four walls are opened, we will get the net of the given figure as shown below.

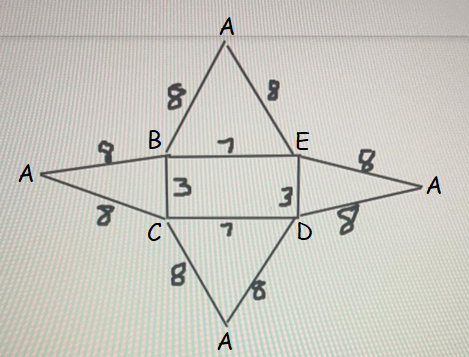
Question 2 :

What are two other names for the line AB in the figure shown below?

Answer :

A line is uni-dimensional shape that extends in both directions infinitely.

In the figure above above AB is a line. Because, it extends in both directions infinitely.

The other names can be given for the line AB in the figure above with the alphabets we have on the line AB.

The other names for the line AB are

BA, AC, BC, etc.,

Question 3 :

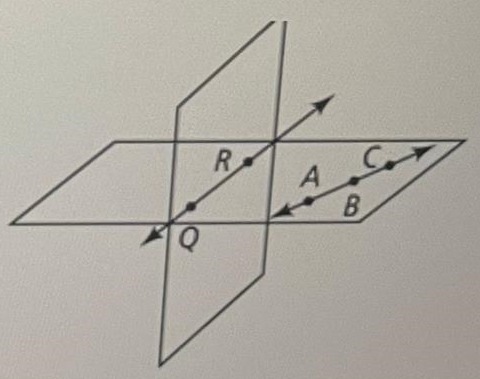
What is the intersection of the two planes?

Answer :

The intersection of two planes above is a line.

In the above figure above, the two planes intersect through the line QR or line RQ.

So, the intersection of the two planes in the figure above is line QR or line RQ.

Question 4 :

B bisects segment AC. Find the value of m.

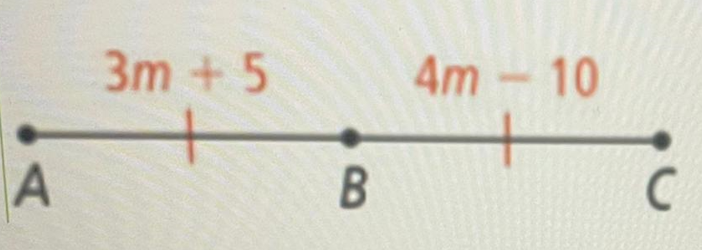
Answer :

Given : B bisects segment AC.

Bisecting means dividing into two equal parts.

Then, the length of AB and Bc must be equal.

AB = BC

3m + 5 = 4m - 10

Subtract 3m from both sides.

5 = m - 10

Add 10 to both sides.

15 = m

or

m = 15

Question 5 :

DG has end points D(-1, 8) and G(3, 4). What are the coordinates of its midpoint?

Answer :

Let a line segment has the following end points.

(x₁, y₁) and (x₂, y₂)

Formula for midpoint of the line segment :

Substitute (x₁, y₁) = D(-1, 8) and (x₂, y₂) = G(3, 4) in the formula above.

The coordinates of midpoint of DG are (1, 6).

Question 6 :

∠1 and ∠2 are supplementary angles. m∠1 is (4y + 7) and ∠2 is (9y + 4). What is m∠2? 

Answer :

Since ∠1 and ∠2 are supplementary,

m∠1 + m∠2 = 180°

(4y + 7) + (9y + 4) = 180

4y + 7 + 9y + 4 = 180

Group and combine the like terms.

(4y + 9y) + (7 + 4) = 180

13y + 11 = 180

Subtract 11 from both sides.

13y = 169

Divide both sides by 13.

y = 13

Given : ∠2 is (9y + 4).

m∠2 = (9y + 4)°

Substitute y = 13.

m∠2 = (9 ⋅ 13 + 4)°

m∠2 = (117 + 4)°

m∠2 = 121°

Question 7 :

Which angle is a vertical angle with ∠ACB? Explain.

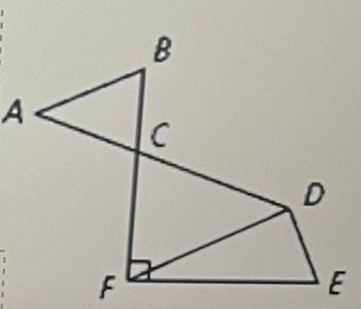
Answer :

Two angles which are opposite to each other at the point of intersection of two lines are called vertical angles.

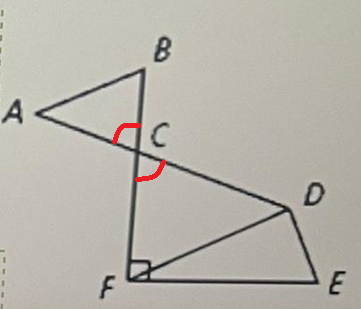
In the figure above, the line segments AD and DF intersect at C.

At the point of intersection C, ∠ACB and ∠FCD are opposite to each other. So, ∠ACB and ∠FCD are vertical angles.

Therefore, ∠FCD is a vertical angle with ACB.

Question 8 :

Name a pair of complementary angles. Explain.

Answer :

In the figure above ∠CFE is a right angle.

m∠CFE = 90°

And also,

m∠CFD + m∠DFE = ∠CFE

m∠CFD + m∠DFE = 90°

Since m∠CFD and m∠DFE add up to 90°, they are complementary angles.

A pair of complementary angles in the figure above is ∠CFD and ∠DFE.

Question 9 :

What is the area of a circle with radius 9 inches. Use 3.14 for π.

Answer :

Formula for area of a circle :

= πr²

Substitute π = 3.14 and r = 9.

= 3.14(9)²

= 3.14(81)

= 254.34 in.²

Question 10 :

Find the area and perimeter of the figure shown below.

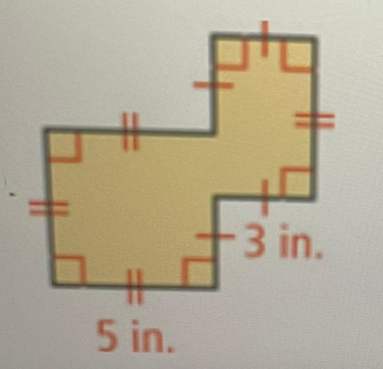
Answer :

Plot the vertices of the given figure above with alphabets A,B, C, D, E, F, G and H. And also, mention the lengths of the segments.

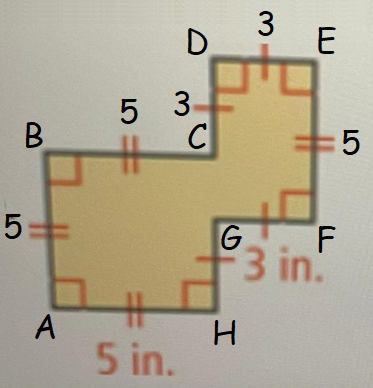
Perimeter of the figure above :

= AB + BC + CD + DE + EF + FG + GH + HA

= 5 + 5 + 3 + 3 + 5 + 3 + 3 + 5

= 32 in.

To get the area of the given figure, divide it into two parts as shown below.

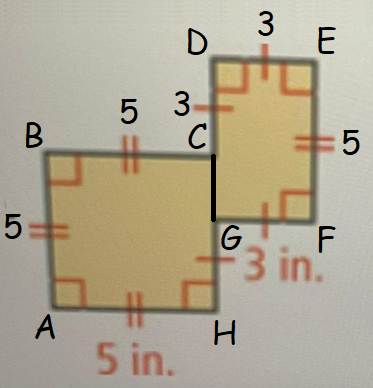
Area of the figure above :

= Area of square ABCH + Area of rectangle GDEF

= side ⋅ side + length ⋅ width

= 5 ⋅ 5 + 3 ⋅ 5

= 25 + 15

= 40 in.²

Question 11 :

∠1 and ∠2 are complementary angles. m∠1 is (5y + 32) and ∠2 is (7y - 14). What is m∠2? 

Answer :

Since ∠1 and ∠2 are complementary,

m∠1 + m∠2 = 90°

(5y + 32) + (7y - 14) = 90

5y + 32 + 7y - 14 = 90

Group and combine the like terms.

(5y + 7y) + (32 - 14) = 90

12y + 18 = 90

Subtract 18 from both sides.

12y = 72

Divide both sides by 12.

y = 6

Given : ∠2 is (7y - 14).

m∠2 = (7y - 14)°

Substitute y = 6.

m∠2 = (7 ⋅ 6 - 14)°

m∠2 = (42 - 14)°

m∠2 = 28°

Question 12 :

Ray GI bisects ∠DGH so that m∠DGI is (3x - 9) and m∠IGH is (2x + 21). Find the m∠DGI.

Answer :

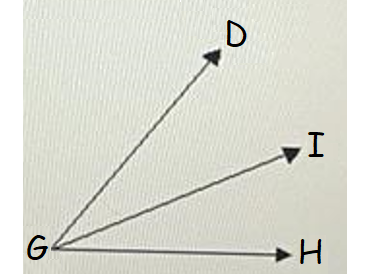
It is given that ray GI bisects ∠DGH. That is, ∠DGH is divided into two equal parts by ray GI.

Then,

m∠DGI = m∠IGH

3x - 9 = 2x + 21

x = 30

It is given that ∠DGI is (3x - 9).

m∠DGI = (3x - 9)°

Substitute x = 30.

m∠DGI = (3 ⋅ 30 - 9)°

m∠DGI = (90 - 9)°

m∠DGI = 81°

Question 13 :

Ray EC bisects ∠BED, m∠AEB = (8x - 4) and m∠CED = (2x + 8). Find m∠AEC.

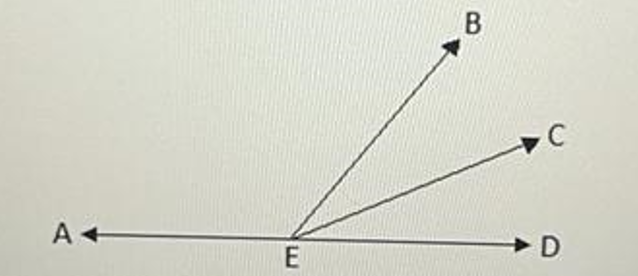
Answer :

It is given that ray EC bisects ∠BED. That is, ∠BED is divided into two equal parts by ray EC.

Then,

m∠BEC = m∠CED

m∠BEC = 2x + 8

∠AEB, ∠BEC and ∠CED together form a straight angle.

∠AEB + ∠BEC + ∠CED = 180°

Equation need to solve for x :

(8x - 4) + (2x + 8) + (2x + 8) = 180

8x - 4 + 2x + 8 + 2x + 8 = 180

12x + 12 = 180

12x = 168

x = 14

∠AEC = ∠AEB + ∠BEC

= (8x - 4) + (2x + 8)

= 8x - 4 + 2x + 8

= 10x + 4

Substitute x = 14.

= 10 ⋅ 14 + 4

= 140 + 4

∠AEC = 144°

Question 14 :

Use the following picture to find the measures of ∠A and ∠B. This is not drawn to scale. Show all your work.

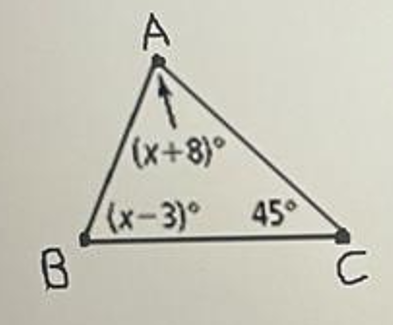
Answer :

The sum of three angles in a triangle is equal to 180°.

∠A + ∠B + ∠C = 180°

(x + 8)° + (x - 3)° + 45° = 180°

x + 8 + x - 3 + 45 = 180

2x + 50 = 180

2x = 130

x = 65

∠A = (x + 8)° = (65 + 8)° = 73°

∠B = (x - 3)° = (65 - 3)° = 62°

Question 15 :

Perform a 90 degree rotation about the origin of the given figure. Be sure to label the points of the image. 

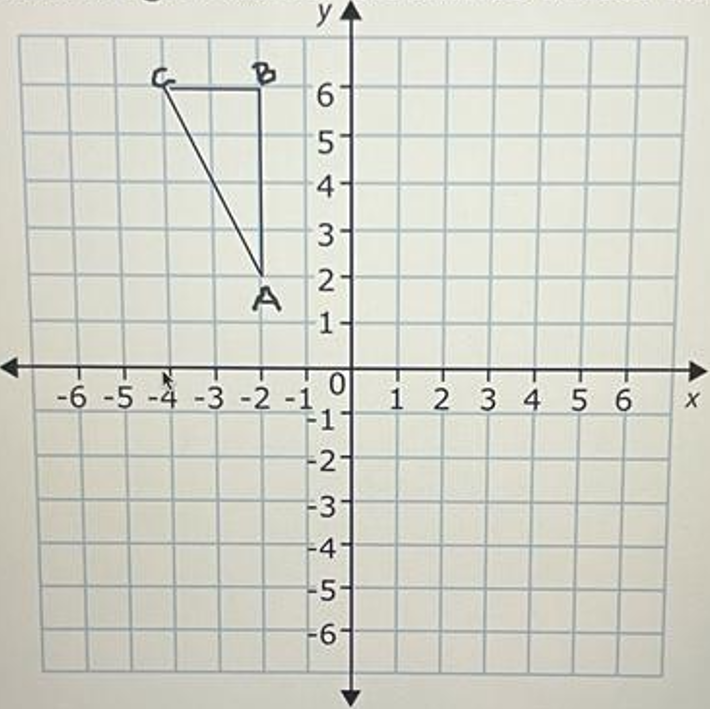
Answer : 

Rule for 90 degree rotation about the origin :

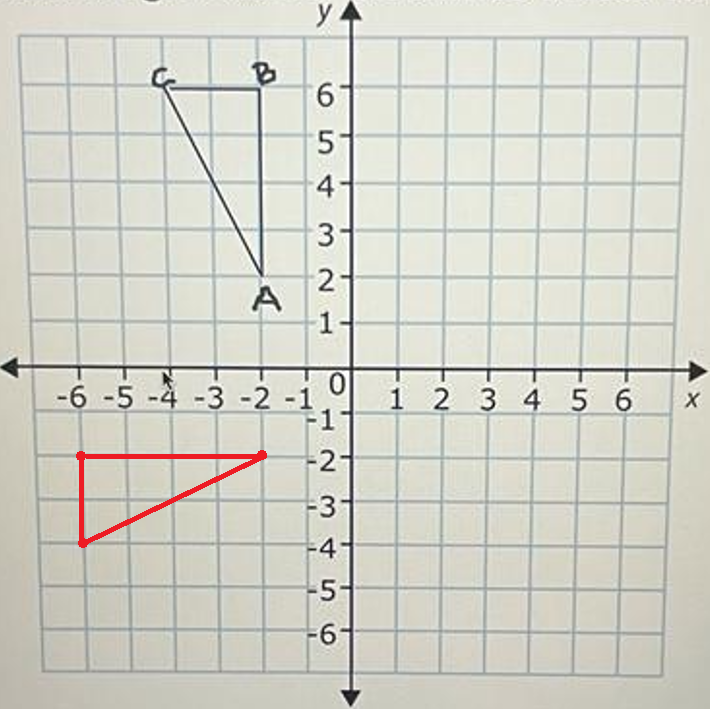
Question 16 :

The point (2, 2) is the image under translation

(x, y) ----> (x + 4, y - 4). What is the preimage of this point?

Answer :

(x + 4, y - 4) = (2, 2)

(x, y) = (-2, 6)

The image of the point (2, 2) is (-2, 6).

Question 17 : 

A dilation has center (0, 0, 0). Find the image of the point (-2, 1, 0) for the scale factor of 3.

Answer :

The image of the point (-2, 1, 0) for the scale factor of 3 :

= (3 ⋅ -2, 3 ⋅ 1, 3 ⋅ 0)

= (-6, 3, 0)

Question 18 : 

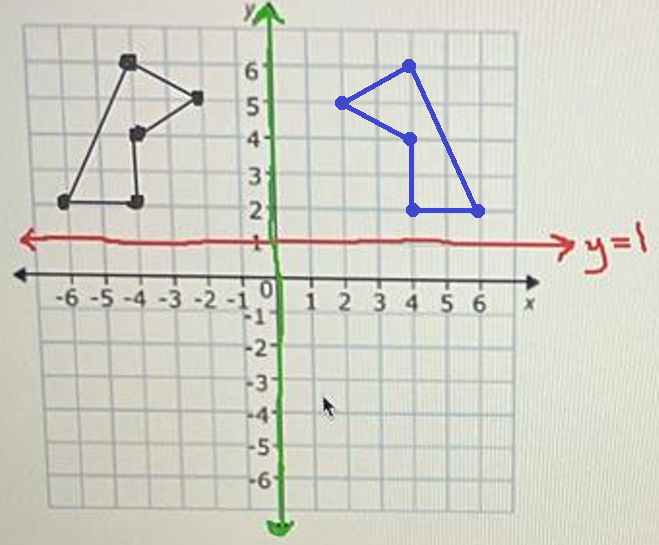
Reflect the image 1st across the y-axis, and then across the line y = 1.

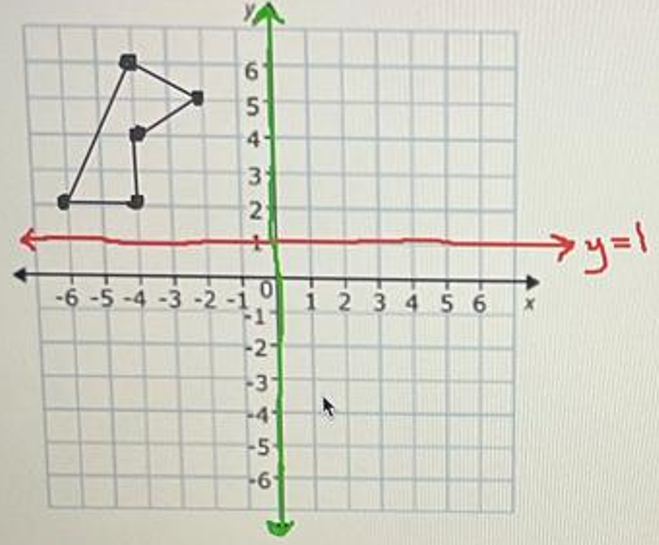
Answer :

Reflection across the y-axis.

Reflection across the line y = 1 :

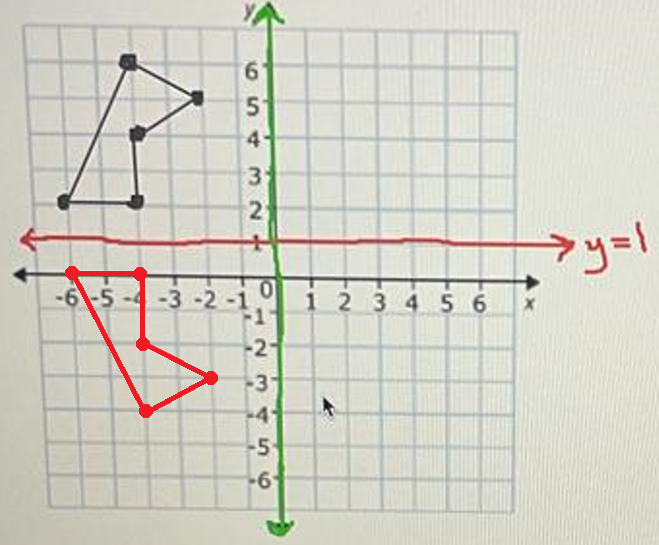
Question 19 : 

Answer the questions from given the following information.

ΔQRS ≅ ΔTUV

RS = 6x - 8

UV = 4x + 2

(a) Write and solve an equation to find the value of x (must show work).

(b) What is the length of RS?

(C) What is the length of UV?

Answer :

Part (a) :

Since ΔQRS ≅ ΔTUV, the corresponding sides must be congruent. Taking the alphabets in both ΔQRS and ΔTUV in order, RS and UV must be congruent. That is, the lengths of RS and UV must be equal.

RS = UV

6x - 8 = 4x + 2

2x - 8 = 2

2x = 10

x = 5

Part (b) :

RS = 6x - 8

Substitute x = 5.

RS = 6 ⋅ 5 - 8

RS = 30 - 8

RS = 22

Part (c) :

UV = 4x + 2

Substitute x = 5.

UV = 4 ⋅ 5 + 2

UV = 20 + 2

UV = 22

Question 20 : 

If ABCD is congruent to LMNO, then BC is congruent to ________.

Answer :

Since ABCD is congruent to LMNO, the corresponding sides must be congruent. Taking the alphabets in both ABCD and LMNO in order, BC must be congruent to MN.

Question 21 : 

Fill in the missing justifications to the proof.

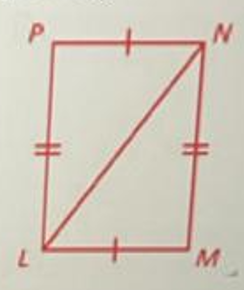
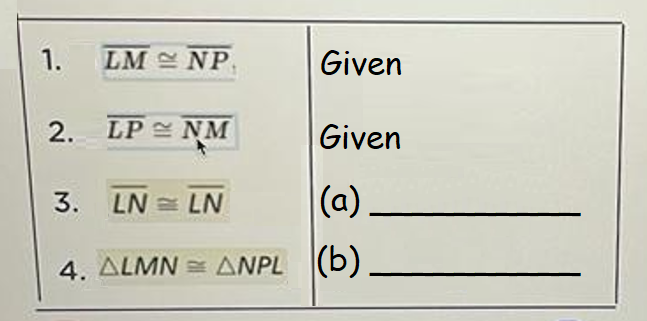
(a) What reason should go in the (a) blank?

a. Transitive Property

b. Reflexive Property

c. Congruence Property

(b) What reason should go in the (b) blank?

a. SSS

b. SAS

c. AAS

Answer :

Part (a) :

c. Congruence Property

Part (b) :

a. SSS

Question 22 : 

Find the value of x and the measure of the angle C.

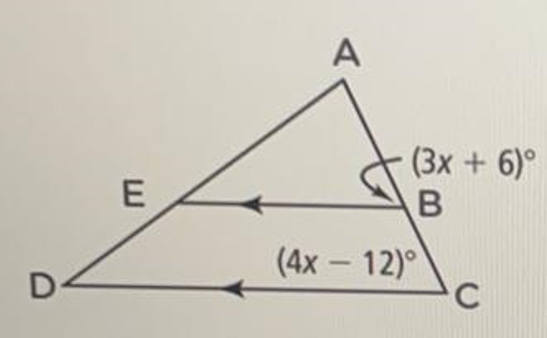
Answer :

In the triangle above, the line segments EB and DC are parallel and AC is the transversal. 

So, ∠ACD and ∠ABE are corresponding angles and their measures are equal.

m∠ACD = ∠ABE

(4x - 12)° = (3x + 6)°

4x - 12 = 3x + 6

x = 18

m∠C = (4x - 12)°

= (4 ⋅ 18 - 12)°

= (72 - 12)°

= 60°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.