APPLICATION OF DIFFERENTIATION MAXIMUM AND MINIMUM

Problem 1 :

Find two positive numbers whose sum is 12 and their product is maximum.

Solution :

Let one number be x. The other number is 12 - x.

Let f(x) be the function

f(x)  =  Product of two numbers

f(x) = x(12 - x)

f(x) = 12x - x²

f'(x) = 12-2x

f'(x) = 0

12-2x = 0

x = 6

f''(x)  =  -2 < 0 Maximum

The first number is 6 and the another number is 6.

Product of two numbers = 36.

Problem 2 :

Find two positive numbers whose product is 20 and their sum is minimum.

Solution :

Let x be the one number, then the another number  =  20/x

Let f(x) be the function.

f(x) = x + (20/x)

f'(x)  =  1 - 20/x²

f'(x)  =  0

1 - 20/x²  =  0

20/x²  =  1

x²  =  20

x  =  2√5

f''(x)  =  -40/x³ < 0

f''(2√5)  =  -1/√5 < 0 (maximum)

Another number  =  20/2√5   =  2√5

So, the sum of numbers  =  2√5 + 2√5  ==>  4√5.

Problem 3 :

Find the smallest possible value of

x² + y²

given that x + y =10.

Solution :

Let f(x) be the function.

Given :

x+y  =  10

y  =  10-x

f(x)  =  x² + y²

f(x)  =  x² + (10-x)²

f(x)  =  x² + 100+x²-20x

f(x)  =  2x²-20x+100

f'(x)  =  4x-20

f'(x)  =  0

4x-20  =  0

x  =  5

f''(x)  =  4(1) ==>  4  > 0 (Minimum)

y  =  10-x

y  =  10-5

y  =  5

x² + y²  =  5² + 5²

x² + y²  =  50

So, the value of x² + y² is 50.

Problem 4 :

A garden is to be laid out in a rectangular area and protected by wire fence. What is the largest possible area of the fenced garden with 40 meters of wire.

Solution :

Let x and y be the length and width of the rectangle.

2(x + y)  =  40

2x + 2y  =  40

2y  =  40-2x

y  =  20 - x

Area of rectangle  =  x(20 - x)

A(x)  =  20x - x²

A'(x)  =  20 - 2x

A'(x)  =  20-2x  =  0

x  =  10

A''(x)  =  -2 < 0 (Maximum)

y  =  20-10

y  =  10

Area  =  10(10)

=  100 m²

So, area of the rectangle is 100 m².

Problem 5 :

A square sheet of cardboard with each side a centimeters is to be used to make an open top box by cutting a small square of cardboard from each of the corners and bending up the sides. What is the side length of small squares if the box is to have large a volume as possible ?

Solution :

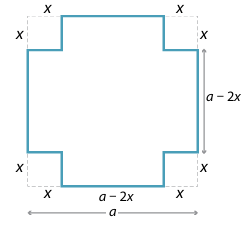
Let x be the side length of small square box.

Volume of the box = length x width x height

= (a - 2x) ⋅ (a - 2x) ⋅ x

V(x) = (a - 2x)² ⋅ x

v'(x) = (a - 2x)² ⋅ (1) + 2(a - 2x) (-2) x

= (a - 2x)² - 4x(a - 2x)

= (a - 2x)[a - 2x - 4x]

v'(x) = (a - 2x)(a - 6x)

v'(x) = 0

(a - 2x)(a - 6x) = 0

v'(x) = (a - 2x)(a - 6x)

v''(x) = (a - 2x)(- 6(1)) + (a - 6x)(0 - 2(1))

= -6(a - 2x) - 2(a - 6x)

= -6a + 12x - 2a + 12x

= -8a + 24x

= 8(3x - a)

To find the maximum value of the function, we have to apply x = a/6 in the function V(x) = (a - 2x)² ⋅ x

V(a/6) = (a - 2(a/6))² ⋅ (a/6)

= (a - (a/3))² ⋅ (a/6)

= ((3a - a)/3))² ⋅ (a/6)

= (2a /3)² ⋅ (a/6)

= (4a²/9) ⋅ (a/6)

= 2a³/27

So, the maximum volume is 2a³/27

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.