APPLYING PROPERTIES OF CHORDS WORKSHEET

To learn the properties of chords in a circle, 

please click here

Problem 1 :  Find the value of y.
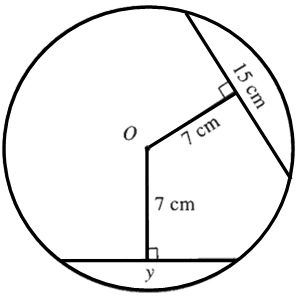Problem 2 :  Find the value of x.
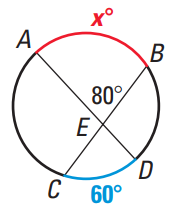Problem 3 :  Find the value of x.
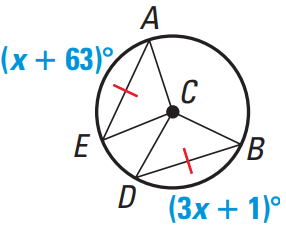Problem 4 :  Find the value of x.
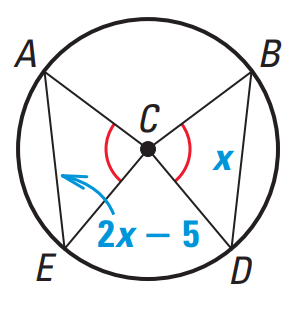Problem 5 :  Find the value of x.
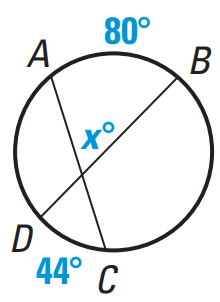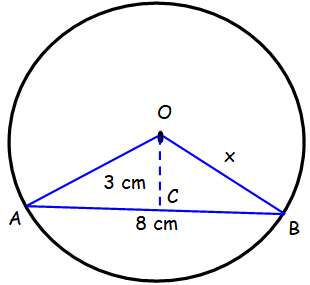
Problem 6 :  Find the value of x.
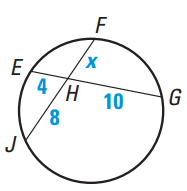
Problem 7 :  Find the value of x.
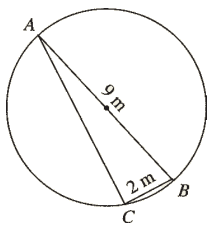
Problem 8 :  Find the value of x.

Solutions

Problem 1 : 

Find the value of y.

Solution :

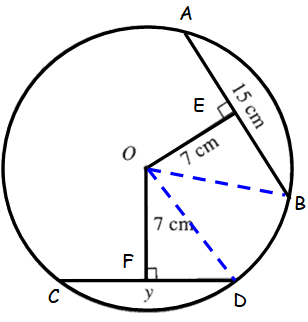
A perpendicular drawn from the center of the circle, bisects the chord.

AE  =  EB  =  15/2  =  7.5 cm

In triangle OEB,

OB²  =  OE² + EB²

OB²  =  7² + (7.5)²

OB²  =  49 + 56.25

OB²  =  105.25

√OB²  =  √105.25

OB  =  10.25 cm

OB  =  OD  =  radius of the circle  =  10.25 cm

In triangle OFD,

OD²  =  OF² + FD²

(10.25)²  =  7² + FD²

105.0625  =  49 + FD²

Subtract 49 from each side. 

56.0625  =  FD²

√56.0265  =  √FD²

7.49  ≈  FD

CD  ≈  2(7.49)

CD  ≈  14.98 cm

So, the value of y is about 14.96 cm.

Question 2 :

Find the value of x. 

Solution :

80°  =  (1/2)[Measure of AB + Measure of CD]

80°  =  (1/2)(x + 60°)

80°  =  (x + 60) / 2

Multiply each side by 2. 

160  =  x + 60

Subtract 60 from each side. 

100  =  x

Question 3 :

Find the value of x. 

Solution :

Because AE  =  BD, 

∠ACE  =  ∠BCD

x + 63  =  3x + 1

Subtract x from each side.

63  =  2x + 1

Subtract 1 from each side.

62  =  2x

Divide each side by 2. 

31  =  x

Question 4 :

Find the value of x.

Solution :

Equal chords of a circle subtend equal angles at the center.

In the above diagram, 

∠ACE  =  ∠BCD

Then

AE  =  BD

2x - 5  =  x

Subtract x from each side.  

x - 5  =  0

Add 5 to each side.  

x  =  5

Question 5 :

Find the value of x.

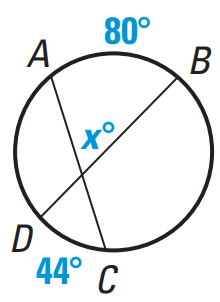
If two chords intersect inside a circle, then the measure of each angle formed is one half the sum of the measures of the arcs intercepted by the angle and its vertical angle.

x  =  (1/2) [measure of arc AB + measure of arc DC]

x  =  (1/2) [80 + 40]

x  =  (1/2)(120)

x  =  60

Question 6 :

Find the values of x.

Perpendicular from the centre of a circle to a chord bisects the chord.

AC  =  BC  =  4 cm

In triangle OCB,

OB²  =  OC² + BC²

x²  =  3² + 4²

x²  =  9 + 16

x²  =  25

x  =  √25

x  =  5 cm

Question 7 :

Find the values of x.

Solution :

EH ⋅ HG  =  JH ⋅ HF

4 ⋅ 10  =  8 ⋅ x

x  =  (4 ⋅ 10) / 8

x  =  40/8

x  =  5

Question 8 :

AB is a diameter of the circle below. If BC = 2 m and AB = 9 m, find the exact length of AC . 

Solution :

In triangle ABC,

∠BCA  =  90° 

By Pythagorean theorem, 

AB²  =  AC² + BC²

9²  =  AC² + 2²

81  =  AC² + 4

Subtract 4 from each side. 

77  =  AC²

√77  =  √AC²

√77  =  AC

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.