AREA AS AN ACCUMULATION PROCESS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question :
The graph of the function g consists of a quarter-circle and three line segments.
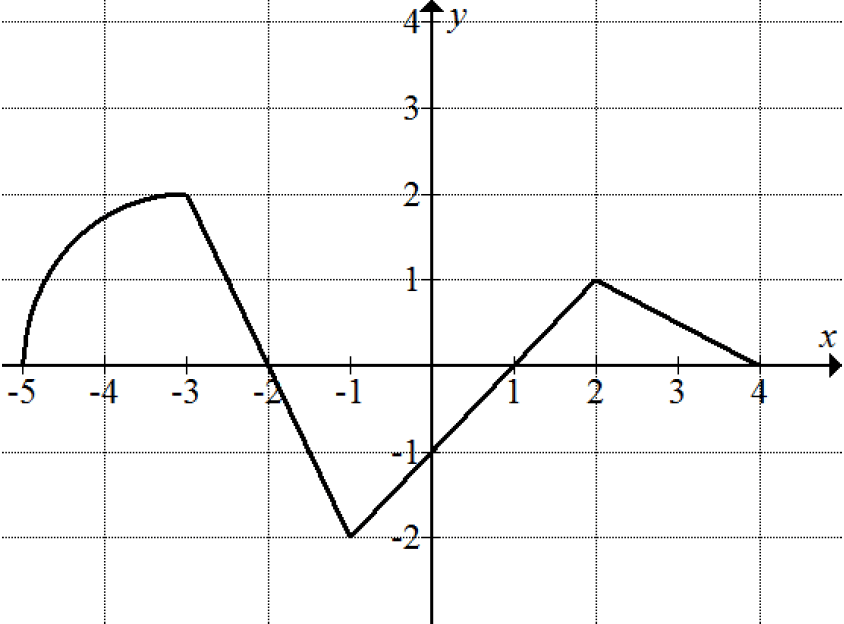
Let f be the function defined by
A. Find f(-5).
B. Find all the values of x on the open interval (5, -4) where f is decreasing. Justify your answer.
C. Write an equation for the line tangent to the graph of f at x = -1.
D. Find the minimum value of f on the closed interval [5, -4]. Justify your answer.
Solution :
Part (A) :
Part (B) :
If f'(x) = 0,
g(x) = 0
In the graph above, g(x) = 0 represents x-intercepts.
The graph intersects x-axis at x = -5, -2, 1 and 4.
When marking these values of x on the number line, we get the following intervals.
(-5, -2), (-2, 1) and (1, 4)
Since we have to find all the values of x on the open interval (5, -4) where f is decreasing, we have to find the interval at where f'(x) or g(x) is negative.
In the above graph, y or g(x) is negative on the open interval (-2, 1).
That is,
f'(x) < 0 when x ∈ (-2, 1).
Therefore, f is decreasing on the open interval
(-2, 1)
Part (C) :
Find the value of y which is corresponding to x = -1. That is f(-1).
y = f(-1) = 0
The point corresponding to x = -1 is (-1, 0).
Slope of the tangent at x = -1.
f'(-1) = g(-1)
From the above graph, g(-1) = -2.
f'(-1) = -2
Slope of the tangent at x = -1 is 2.
The tangent line to the graph of f is passing through the point (-1, 0) with the slope -2.
Equation of a line through the point (x1, y1) with the slope m :
y - y1 = m(x - x1)
Substitute (x1, y1) = (-1, 0) and m = -2.
y - 0 = -2[x - (-1)]
y = -2(x + 1)
y = -2x - 2
Equation for the line tangent to the graph of f at x = -1 is
y = -2x - 2
Part (D) :
Already we got the values of x when f'(x) = 0. They are
x = -5, -2, 1 and 4
The above set of values of x includes the extreme values of the closed interval [-5, 4].
We have to find the value of x for which f(x) is minimum.
When x = -5,
When x = -2,
When x = 1,
When x = 4,
Compare the above four values of f(x) :
f(-5) = -π or -3.14
f(-2) = 1
f(1) = -2
f(4) = 0
In the above four values of f(x), the minimum value is -π when x = -5.
The minimum value of f on the closed interval [-5, 4] is -π.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37) -
Factorial Problems and Solutions
Dec 02, 25 09:27 AM
Factorial Problems and Solutions -
10 Hard SAT Math Questions (Part - 36)
Nov 28, 25 09:55 AM
10 Hard SAT Math Questions (Part - 36)

