AREA OF TRIANGLE USING SINE FORMULA

Area of the triangle is a half of product of two sides and the side included angle.

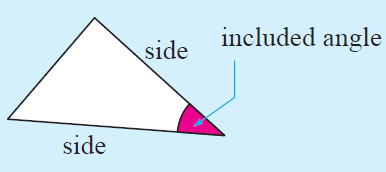
Consider the triangle given below, in which the sides opposite angles A, B and C are labelled a, b and c respectively.

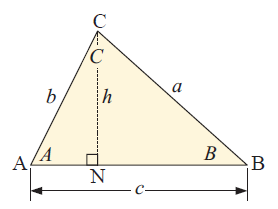
In the triangle given above

AB  =  c (base) and

CN  =  h(height)

In triangle ANC,

sin A  =  Opposite side / hypotenuse

sin A  =  h/b

h  =  b (sin A)

So, area of triangle ABC  =  (1/2) ⋅ base ⋅ height

=  (1/2) ⋅ c ⋅ (b sin A)

Area of triangle  =  (1/2) ⋅ (bc sin A)

Find the area of the triangle given below :

Example 1 :

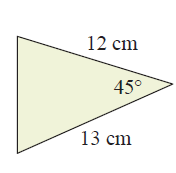
Solution :

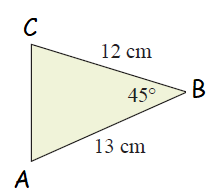
<B  =  45, a  =  12 cm and c  =  13 cm.

Area of triangle  =  (1/2) ⋅ (ac sin B)

=  (1/2) ⋅ (13) ⋅ (12) sin 45

=  (1/2) ⋅ (13) ⋅ (12) (0.707)

=  55.146 cm²

Example 2 :

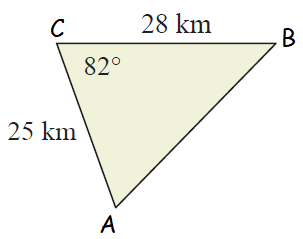
Solution :

<C  =  82, a  =  28 km and c  =  25 km

Area of triangle  =  (1/2) ⋅ (ac sin C)

=  (1/2) ⋅ (28) ⋅ (25) sin 82

=  (1/2) ⋅ (28) ⋅ (25) (0.990)

=  346.5 km²

So, the area of the given triangle is 347 km².

Example 3 :

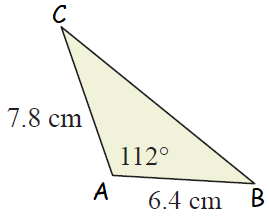
Solution :

<A  =  112, c  =  6.4 cm and b  =  7.8 cm

Area of triangle  =  (1/2) ⋅ (bc sin A)

=  (1/2) ⋅ (7.8) ⋅ (6.4) sin 112

=  (1/2) ⋅ (7.8) ⋅ (6.4) (0.927)

=  23.13 cm²

So, the area of the given triangle is 23.13 cm².

Example 4 :

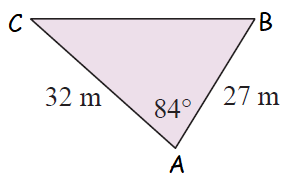
Solution :

<A  =  84, b  =  32 m and c  =  27 m

Area of triangle  =  (1/2) ⋅ (bc sin A)

=  (1/2) ⋅ (32) ⋅ (27) sin 84

=  (1/2) ⋅ (32) ⋅ (27) (0.994)

=  429.40 m²

So, the area of the given triangle is 430 cm².

Example 5 :

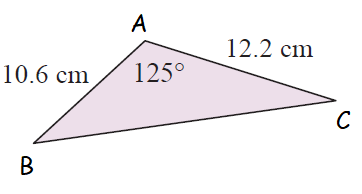
Solution :

<A  =  125, b  =  12.2 cm and c  =  10.6 cm

Area of triangle  =  (1/2) ⋅ (bc sin A)

=  (1/2) ⋅ (12.2) ⋅ (10.6) sin 125

=  (1/2) ⋅ (12.2) ⋅ (10.6) (0.819)

=  52.95 cm²

So, the area of the given triangle is 53cm².

Example 6 :

Find the area of a parallelogram with sides 6.4 cm and 8.7 cm and one interior angle 64^o.

Solution :

In a parallelogram, opposite angles are equal and opposite sides are equal.

So, by drawing the diagonal we can divide the parallelogram into two triangles of equal area.

<A  =  64, b  =  6.4 cm and c  =  8.7 cm

Area of triangle  =  (1/2) ⋅ (bc sin A)

=  (1/2) ⋅ (6.4) (8.7) sin 64

=   (1/2) ⋅ (6.4) (8.7) (0.898)

=  25

Area of parallelogram  =  2(25)

=  50 cm²

Problem 7 :

If triangle ABC has area 150 cm², find the value of x.

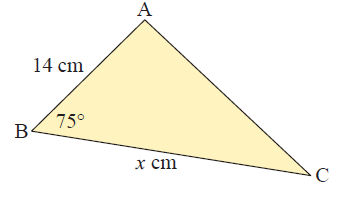
Solution :

<B  =  75, a  =  x cm and c  =  14 cm

Area of triangle  =  (1/2) ⋅ (ac sin B)

=  (1/2) ⋅ (x) (14) sin 75

=   7x (0.965)

=  6.755x

6.755x  =  150

x  =  150/6.755

x  =  22.2 cm

So, the value of x is 22.2 cm.

Problem 8 :

A parallelogram has two adjacent sides with lengths 4 cm and 6 cm respectively. If the included angle measures 52 degree, find the area of the parallelogram.

Solution :

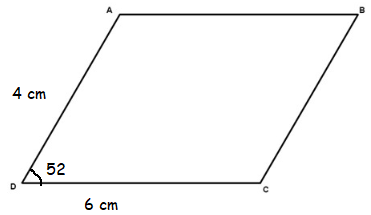
Area of triangle  =  (1/2) ⋅ (ac sin B)

here a = 6 cm, c = 4 cm and B = 52

=  (1/2) ⋅ (6) (4) sin 52

= 12  sin 52

= 12(0.788)

= 9.456

Area of parallelogram = 9.456(2)

= 18.912 cm²

So, the required area of parallelogram is 18.9 cm²

Problem 9 :

A rhombus has sides of length 12 cm and an angle of 72 degree. Find its area. 

Solution :

Since the given shape is a rhombus, all sides will be equal. By finding area of one triangle and multiplying the result by 2, we will get area of rhombus.

Area of triangle = 1/2 x 12 x 12 x sin 72

= 72 sin 72

= 72(0.951)

= 68.472 cm²

Area of rhombus = 2(68.472)

= 136.944 cm²

Problem 10 :

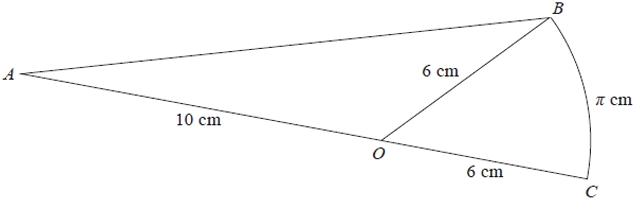
Shows a shape ABC in which AOB is a triangle, AOC is a straight line and OBC is a sector of a circle with centre O. AO = 10 cm, OC = OB = 6 cm and the length of arc BC = π cm. Find, to 3 significant figures

(a) the length of AB

(b) the area of the shape ABC.

Solution :

a)

Length of arc = (θ/360) x 2πr

radius = 6 cm

π = (θ/360) x 2π(6)

1 = (θ/360) x 12

1 = (θ/30)

θ = 30

<AOB = 180 - 30

= 150

AB² = OA² + OB² - 2 (OA)(OB) cos 150

AB² = 10² + 6² - 2 (10)(6) cos 150

= 100 + 36 - 120(-0.866)

= 136 + 103.92

= √239.92

AB = 15.5 cm

b) Area of ABC = Area of triangle AOB + area of OBC

Area of triangle = (1/2) x b x c sin θ

Area of sector OBC = (θ/360) x πr²

= (1/2) x 10 x 6 x sin 150 + (30/360) x 3.14 x 6²

= 30 (0.5) + 9.42

= 15 + 9.42

= 24.42

Problem 11 :

A rhombus has an area of 50 cm² and an internal angle of size 63 degree. Find the length of its sides.

Solution :

Area of rhombus

= 2 x (1/2) product of adjacent sides x sin θ

For a rhombus, all sides will be equal.

50 = a² x sin 63

50 / sin 63 = a²

50/0.89 = a²

a² = 56.17

a = √56.17

a = 7.49

a = 7.5 cm

So, side length of rhombus is 7.5 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.