ARITHMETIC PROBLEMS WITH SOLUTIONS FOR COMPETITIVE EXAMS

Question 1 :

Which of the following is not even ?

(A)  330  (B)  436  (C)  752  (D)  861  (E)  974

Solution :

If the given number is even, then it must ends with one of the following numbers 0, 2, 4, 6 or 8.

In the above numbers 861 ends with 1, which is not even. Hence 861 is not even number.

Question 2 :

 What is the least prime number greater than 50 ?

(A)  51  (B)  53  (C)  55  (D)  57  (E)  59

Solution :

A number which is divisible by 1 and itself is known as prime numbers. 

51 is divisible by 1, 51, 3, 7. So it not prime.

53 is divisible by 1 and 53. There is no divisor other than 1 and 53. Hence it is prime.

Question 3 :

Which of the following is a multiple of 2 ?

(A)  271  (B)  357   (C)  463  (D)  599  (E)  756

Solution :

Multiple of 2 is also even number. Since 756 is even number, it is multiple by 2. 

Question 4 :

(15 ⋅ 7 ⋅ 3) / (9 ⋅ 5 ⋅ 2)  =  

(A)  2/7  (B)  3/5  (C)  3  1/2  (D)  7  (E)  7  1/2

Solution :

=  (15 ⋅ 7 ⋅ 3) / (9 ⋅ 5 ⋅ 2)

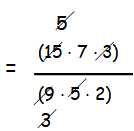
=  7/2

By converting the improper fraction as mixed fraction, we get 3  1/2.

Question 5 :

What is the lest common multiple of 18 and 24 ?

(A)  6  (B)  54  (C)  72  (D)  96  (E)  432

Solution :

To find L.C.M of 18 and 24, let us use "ladder method"

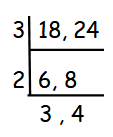
LCM of 18 and 24  =  3 ⋅ 2 ⋅ 3 ⋅ 4

  =  72

Question 6 :

Which of the following is a multiple of 3 ?

(A)  115  (B)  370  (C)  465  (D)  589  (E)  890

Solution :

In order to find which of the following number is a multiple of 3, let us use divisibility test.

Divisibility rule of 3 :

If the sum of the digits is a multiple of 3, then the given number is divisible by 3. 

115  =  1 + 1 + 5  =  7 (not divisible by 3)

370  =  3 + 7 + 0  =  10 (not divisible by 3)

465  =  4 + 6 + 5  =  15 (divisible by 3)

Hence 465 is a multiple of 3.

Question 7 :

-6 (3 - 4 ⋅ 3)  =  

(A)  -66  (B)  -54  (C)  -12  (D)  18  (E)  54

Solution :

According to order of operation, first we have to consider the parenthesis. (BODMAS)

   =  -6 (3 - 4 ⋅ 3) (performing multiplication)

  =  -6(3 - 12)

  =  -6 (-9)

  =  54

Hence the answer is 54.

Related pages

• Arithmetic Quiz Questions

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.