AVERAGE SPEED FORMULA

Average speed formula is used to find the  uniform rate which involves something travelling at fixed and steady pace.

For example, A car travels 3 hours. It travels 30 miles in the first hour, 45 miles in the second hour and 75 miles in the third hour.

speed in the first hour = 30 miles/hour

speed in the second hour = 45 miles/hour

speed in the third hour = 75 miles/hour

We have three different speeds in  the three hour journey.

If we want to find the average speed for the whole journey of three hours, we have to find the ratio between the total distance covered and total time taken.

That is,

constant speed = (30 + 45 + 75)/3

= 150/3

= 50 miles/hour 

Based on the above example, the formula is to find the average speed is given below.

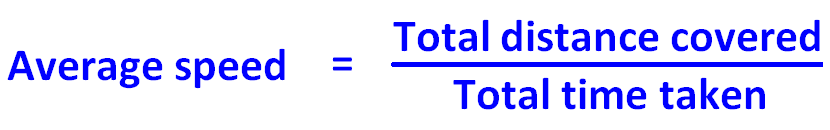
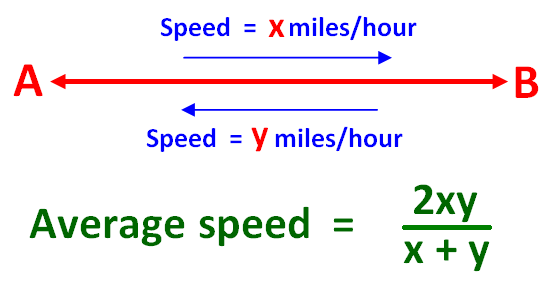
If a person travels from A to B at some speed, say x miles per hour. He comes back from B to A at different speed, say y miles per hour. Both the ways, he covers the same distance, but at different speeds.

Then, the formula is to find the average speed for the whole journey is given below.

Example 1 :

David drove for 3 hours at a rate of 50 miles per hour, for 2 hours at 60 miles per hour and for 5 hours at a rate of 70 miles per hour. What was his average speed for the whole journey?

Answer :

Step 1 :

Formula for average speed is

= Total distance/Total time taken

And also, formula for the distance is

= Rate ⋅ Time

Step 2 :

Distance covered in the first 3 hours is

= 50 ⋅ 3

= 150 miles

Distance covered in the next 2 hours is

= 60 ⋅ 2

= 120 miles

Distance covered in the last 5 hours is

= 70 ⋅ 5

= 350 miles

Step 3 :

Then, total distance is

= 150 + 120 + 350

= 620 miles

Total time is

= 3 + 2 + 5

= 10 hours

Step 4 :

So, the average speed is

= 620/10

= 62

So, the average speed for the whole journey is 62 miles per hour.

Example 2 :

Jose travels from the place A to place B at a certain speed. When he comes back from place B to place A, his speed is 60 miles per hour. If the average speed for the whole journey is 72 miles per hour, find his speed when he travels from the place A to B.

Answer :

Step 1 :

Let a be the speed from place A to B.

Speed from place B to A = 60 miles/hour.

Step 2 :

Here, both the ways, he covers the same distance.

Then, formula to find average speed is

= 2xy/(x + y)

Step 3 :

x ----> speed from place A to B

x = a

y ----> speed from place B to A

y = 60

Step 4 :

Given : Average speed  is 72 miles/hour.

(2 ⋅ a ⋅ 60)/(a + 60) = 72

120a = 72(a + 60)

120a = 72a + 4320

48a = 4320

a = 90

So, the speed from place A to B is 90 miles per hour.

Example 3 :

David travels from the place A to place B at a certain speed. When he comes back from place B to place A, he increases his speed 2 times. If the constant-speed for the whole journey is 80 miles per hour, find his speed when he travels from the place A to B.

Answer :

Step 1 :

Let a be the speed from place A to B.

Then, speed from place B to A = 2a

Step 2 :

The distance traveled in both the ways (A to B and B to A) is same.

So, the formula to find average speed is

= 2xy/(x + y)

Step 3 :

x ----> Speed from place A to B

x = a

y ----> Speed from place B to A

y = 2a

Step 4 :

Given : Average speed = 80 miles/hour

(2 ⋅ a ⋅ 2a)/(a + 2a) = 80

4a²/3a = 80

4a/3 = 80

a = 60

So, the speed from place A to B is 60 miles per hour.

Example 4 :

A person takes 5 hours to travel from place A to place B at the rate of 40 miles per hour. He comes back from place B to place A with 25% increased speed. Find the average speed for the whole journey.

Answer :

Step 1 :

Speed (from A to B) = 40 miles/hour

Speed (from B to A) = 50 miles/hour (25% increased)

Step 2 :

The distance traveled in both the ways (A to B and B to A) is same.

So, the formula to find average distance is

= 2xy/(x + y)

Step 3 :

x ----> speed from place A to B

x = 40

y ----> speed from place B to A

y = 50

Step 4 :

Average speed = (2 ⋅ 40 ⋅ 50)/(40 + 50)

= 44.44

So, the average speed for the whole journey is about 44.44 miles/hour.

Example 5 :

Speed (A to B) = 20 miles/hour

Speed (B to C) = 15 miles/hour

Speed (C to D) = 30 miles/hour

If the distances from A to B, B to C and C to D are equal and it takes 3 hours to travel from A to B, find the average speed from A to D.

Answer :

Step 1 :

Formula to find distance is

= Rate ⋅ Time

Distance from A to B is

= 20 ⋅ 3

= 60 miles

Given : Distance from A to B, B to C and C to D are equal.

Total distance from A to D is

= 60 + 60 + 60

= 180  miles

Step 2 :

Formula to find time is

= Distance/Speed

Time (A to B) = 60/20 = 3 hours

Time (B to C) = 60/15 = 4 hours

Time (C to D) = 60/30 = 2 hours

Total time taken from A to D is

= 3 + 4 + 2

= 9 hours

Step 3 :

Formula to find average speed is

= Total distance/Total time

= 180/9

= 20

So, the average speed from A to D is 20 miles per hour.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.