BASIC PROPORTIONALITY THEOREM AND ITS CONVERSE WORKSHEET

(1)  In figure given below  DE ∥ BC. Find EC in (i) and AD in (ii)

Solution

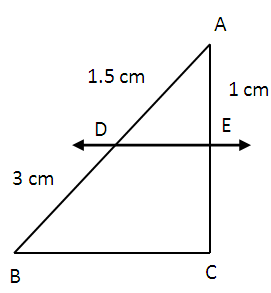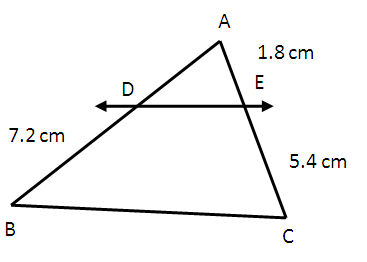(2) E and F are points on the sides PQ and PR respectively of a ∆ PQR. For each of the following cases, state whether EF ∥ QR.

(i) PE  =  3.9 cm , EQ  =  3 cm, PF  =  3.6 cm and FR  =  2.4 cm

(ii) PE  =  4 cm , EQ  =  4.5 cm, PF  =  8 cm and FR  =  9 cm

(iii) PQ  =  1.28 cm PR  =  2.56 cm PE  =  0.18 cm and  PF  =  0.36 cm  

Solution

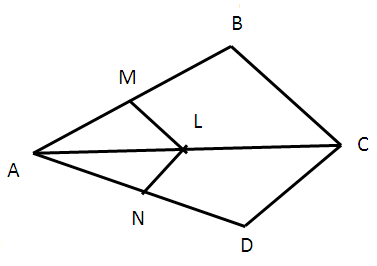
(3) In the figure given below, if LM ∥ CB and LN ∥ CD prove that (AM/AB)  =  (AN/AD)

Solution

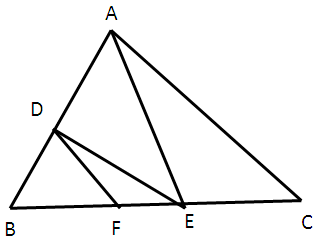
(4)  DE ∥ AC and DF ∥ AE. prove that (BF/FE)  =  (BE/EC)

Solution

(5)  In the figure given below , DE ∥ OQ and DF ∥ OR. Show that EF ∥ QR

Solution

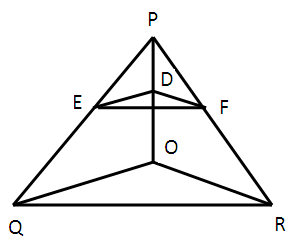
(6) In fig 6.21, A,B and C are points on OP,OQ and OR respectively such that AB ∥ PQ and AC ∥ PR.Show that BC ∥ QR

Solution

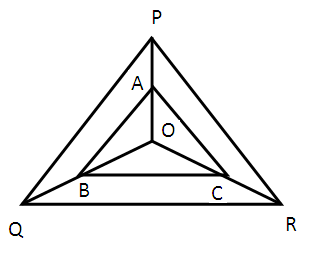
(7)  ABCD is a trapezium in which AB ∥ DC and its diagonals intersect each other at the point O. Show that (AO/BO) = (CO/DO)         Solution

(8) The diagonals of a quadrilateral ABCD intersect each other at the point O such that (AO/BO)  = (CO/D0). show that ABCD is a trapezium.         Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.