CHANGE OF BASE IN LOGARITHM
Before learning how to change of the base of a logarithm, you need to be aware of the multiplication of two logarithms.
Two logarithms can be multiplied, if one of the following two conditions is met.
Condition (i) :
The argument of the first logarithm and the base of the second logarithm must be same.
Condition (ii) :
The base of the first logarithm and the argument of the second logarithm must be same.
Example 1 :
Simplify : logab ⋅ logbc
In the above two logarithms, the argument of the first logarithm and the base of the second logarithm are same.
So, we can simplify the multiplication of above two logarithms by removing the part circled in red color.
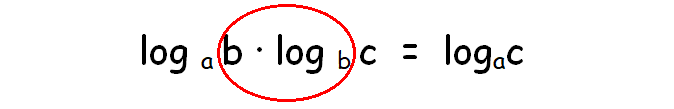
Example 2 :
Simplify : logxy ⋅ logzx
In the above two logarithms, the base of the first logarithm and the argument of the second logarithm are same.
So, we can simplify the multiplication of above two logarithms by removing the part marked in red color.
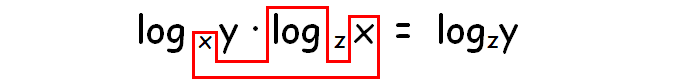
How to Change Base of a Logarithm
For some purposes, we may find it useful to change from logarithm in one base to logarithm in another base.
Suppose we are given logax and want to find logbx.
We can write logax as a product of two logarithms with desired base in the first logarithm.
logax = logbx ⋅ logab
Now, move the second logarithm (logab) in the above product to denominator. We already know, if a logarithm is moved from numerator to denominator or denominator to numerator, we have to switch the argument and base.
Then, we have
logax = (logbx)/(logba)
Now, look at the base of the two logarithms on the right side, it is 'b'.
In this way, we can change the given base of a logarithm to any desired base.
But, always we don't have to write the given logarithm as a product of two logarithms. For understanding purpose, change of base is explained using the product of two logarithms above.
We can do this more quickly. Consider the logarithm given below.
logba
In the logarithm above, the base is 'b'. If we want to change the base, write two logarithms in division with the arguments 'a' in the logarithm in numerator and argument 'b' in the logarithm in denominator. And then, whatever base we want, we can take for the logarithms in numerator and denominator. But, the same base should be taken for both the logarithms.
For example, in logba, if we want to change the base to 'x', we can do it as shown below.
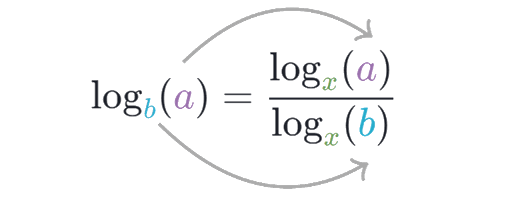
In the above example, the base of the given logarithm 'b' is changed to 'x'.
In this way, we can change the base of the given logarithm to any other base.
Solved Problems
Problem 1 :
If the value of log102 = 0.3010, find the value of log25.
Solution :
Given : log102 = 0.3010.
The value of log102 is given and its base is 10.
So, change the base of log25 to 10.
log25 = (log105)/(log102)
= [log10(10/2)]/(log102)
= (log1010 - log102)/(log102)
= (1 - 0.3010)/0.3010
= 0.6990/0.3010
≈ 2.3223
Problem 2 :
Simplify the following expression and give your answer in terms of logarithm to the base 10.
Solution :
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Resources (Videos, Concepts, Worksheets and More)
Dec 23, 24 03:47 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 91)
Dec 23, 24 03:40 AM
Digital SAT Math Problems and Solutions (Part - 91) -
Digital SAT Math Problems and Solutions (Part - 90)
Dec 21, 24 02:19 AM
Digital SAT Math Problems and Solutions (Part - 90)