CHECK IF THE GIVEN QUADRILATERAL IS CYCLIC OR NOT
The given quadrilateral is a cyclic quadrilateral if one of the following is true.
- One pair of opposite angles is supplementary.

- If α + β = 180 then ABCD is a cyclic quadrilateral.
One side subtends equal angles at the other two vertices.
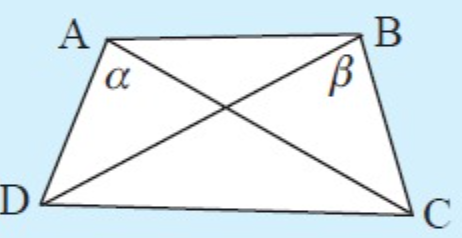
- If α = β then ABCD is a cyclic quadrilateral.
Is ABCD a cyclic quadrilateral ? Explain your answers.
Example 1 :
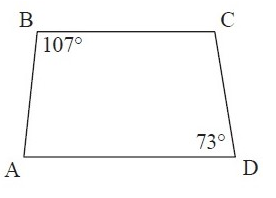
Solution :
By observing the figure, m<B and m<D are opposite angles.
So,
m<B + m<D = 107˚ + 73˚
m<B + m<D = 180˚ (supplementary angles)
So, there is one pair of opposite angles that are supplementary.
Yes, it is a cyclic quadrilateral.
Example 2 :
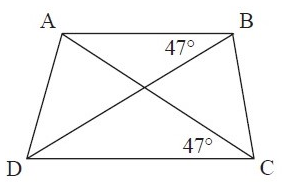
Solution :
In the figure, m<B = m<c = 47˚
So, m<A and m<D subtends equal angles at <B and <C
Yes, it is a cyclic quadrilateral.
Example 3 :
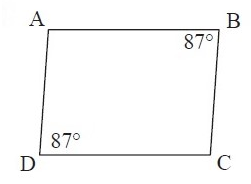
Solution :
By observing the figure, m<B and m<D are opposite angles.
So,
m<B + m<D = 87˚ + 87˚
m<B + m<D = 174˚ (not supplementary angles)
There is one pair of opposite angles that are not supplementary.
So, it is not a cyclic quadrilateral.
Example 4 :
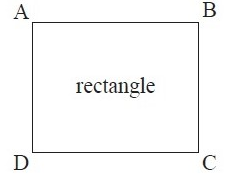
Solution :
By observing the figure, it is a rectangle (all the angles are 90˚).
Then, m<B and m<D are opposite angles.
m<B + m<D = 90˚ + 90˚
m<B + m<D = 180˚(supplementary angles)
So, opposite angles are supplementary.
Yes, it is a cyclic quadrilateral.
Example 5 :
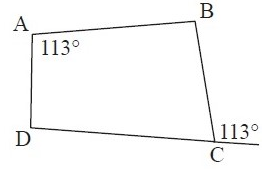
Solution :
In the figure, m<A and m<E = 113˚(interior and exterior angle)
The sum of the interior angle of a triangle is 180˚
180˚ - <C = 113˚
180˚ - 113˚ = <C
<C = 67˚
Now, m<A and m<C are opposite angles.
m<A + m<C = 113˚ + 67˚
m<A + m<C = 180˚ (supplementary angles)
So, there is one pair of opposite angles that are supplementary.
Yes, it is a cyclic quadrilateral.
Example 6 :
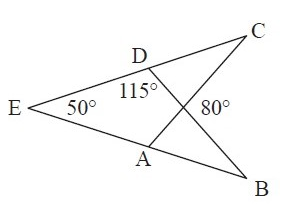
Solution :
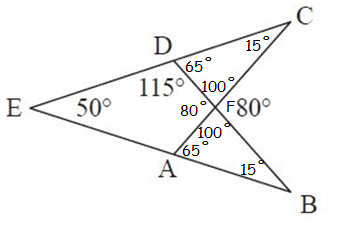
By vertically opposite angles,
<BFC = <AFD = 80˚
<DFC = <AFB (adjacent angle)
We know that vertical angle and its adjacent angle are supplementary angles)
<BFC + <DFC = 180˚
80˚ + <DFC = 180˚
<DFC = 180˚ - 80˚
= 100˚
<DFC = <AFB = 100˚
By linear pair of angles,
<EDB = 115˚
<EDB + <CDB = 180˚
<CDB = 180˚ - <EDB
<CDB = 180˚ - 115˚
<CDB = 65˚
In ∆DFC,
<FDC + <DFC + <DCF = 180˚
100˚ + 65˚ + <DCF = 180˚
<DCF = 180˚ - 165˚
<DCF = 15˚
We know that the angle subtended by the same arc are equal.
<CDB = <CAB = 65˚
<DCA = <DBA = 15˚
m<B = m<c = 15˚
So, m<A and m<D subtends equal angles at <B and <C
Yes, it is a cyclic quadrilateral.
Example 7 :
ABCD is a cyclic parallelogram. Show that it is a rectangle.
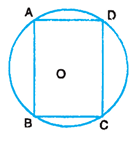
Solution :
Given that ABCD is a cyclic quadrilateral, then sum of opposite angles will be equal to 180o.
∠A + ∠C = 180o ----(1)
Since it is parallelogram, the opposite sides are equal and opposite angles are also equal.
∠A = ∠C
applying in (1), we get
∠A + ∠A = 180o
2∠A = 180o
∠A = 180o / 2
= 90o
So, the given is a rectangle.
Example 8 :
A pair of opposite sides of a cyclic quadrilateral is equal. Prove that its diagonals are also equal
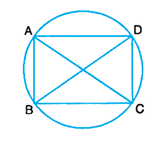
Solution :
Let ABCD be a cyclic quadrilateral and AB = CD.
arc AB = arc CD (Corresponding arcs)
Adding arc AD to both the sides;
arc AB + arc AD = arc CD + arc AD
∴ arc BAD = arc CDA
Chord BD = Chord CA ⇒ BD = CA
Example 9 :
In Figure PQRS is a cyclic quadrilateral whose diagonals intersect at A. If ∠SQR = 80o and ∠QPR = 30o, find ∠SRQ.
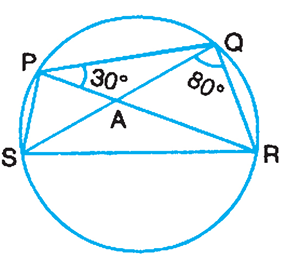
Solution :
∠SQR = 80o and ∠QPR = 30o
∠SQR = 80o = ∠SPR
Angles created by the same arc PS
∠QPR = 30o = ∠QSR
Angles created by the same arc QR
In triangle SQR,
∠QSR + ∠SQR + ∠SRQ = 180
30 + 80 + ∠SRQ = 180
110 + ∠SRQ = 180
∠SRQ = 180 - 110
∠SRQ = 70
Example 10 :
PQRS is a cyclic quadrilateral. If ∠Q = ∠R = 65o , find ∠P and ∠S.
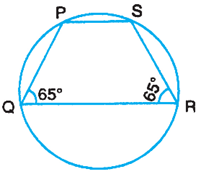
∠P + ∠R = 180o
∠P = 180o – ∠R
= 180o – 65o
∠P = 115o
Similarly, ∠Q + ∠S = 180o
∠S = 180o – ∠Q
= 180o – 65o
∠S = 115o
Example 11 :
In Figure, ABCD is a cyclic quadrilateral whose diagonals intersect at O. If ACB = 50o and ∠ ABC = 110o, find ∠ BDC.
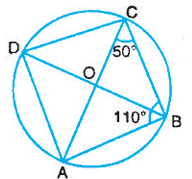
Solution :
In triangle ABC,
∠BAC + ∠ABC + ∠BCA = 180
∠BAC + 110 + 50 = 180
∠BAC + 160 = 180
∠BAC = 180 - 160
∠BAC = 20
∠BDC = 20
Angles created by the same arc BC.
Example 12 :
In Figure, PQRS is a cyclic quadrilateral, and the side PS is extended to the point A. If ∠PQR = 80o, find ∠ASR.
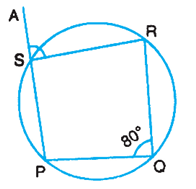
Solution :
Since the given shape is a cyclic quadrilateral,
∠PQR + ∠PSR = 180
80 + ∠PSR = 180
∠PSR = 180 - 80
∠PSR = 100
∠ASR and ∠PSR are supplementary.
Then ∠ASR = 80
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 8)
Feb 05, 25 12:22 PM
AP Calculus AB Problems with Solutions (Part - 8) -
AP Calculus AB Problems with Solutions (Part - 9)
Feb 05, 25 12:15 PM
AP Calculus AB Problems with Solutions (Part - 9) -
Digital SAT Math Problems and Solutions (Part - 106)
Feb 04, 25 08:16 AM
Digital SAT Math Problems and Solutions (Part - 106)
