COMPARING SLOPES OF TWO LINES

A line’s slope is a measure of its steepness. Some lines are steeper than others. As the absolute value of the slope increases, the line becomes steeper. As the absolute value of the slope decreases, the line becomes less steep.

Example 1 : 

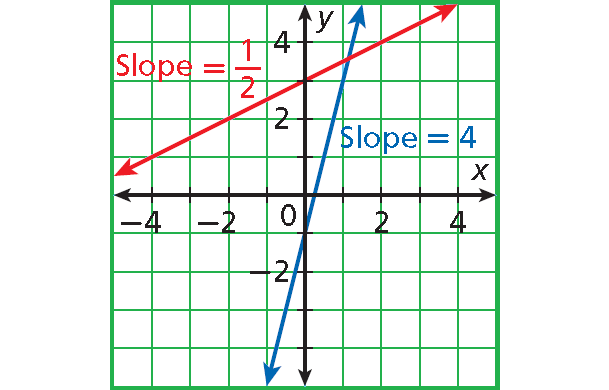
Solution : 

The line with slope 4 is steeper than the line with slope 1/2.

|4| > |1/2|

Example 2 : 

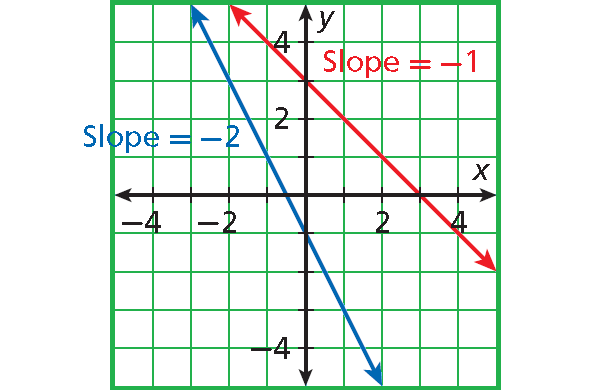
Solution : 

The line with slope -2 is steeper than the line with slope -1.

|-2| > |-1|

Example 3 : 

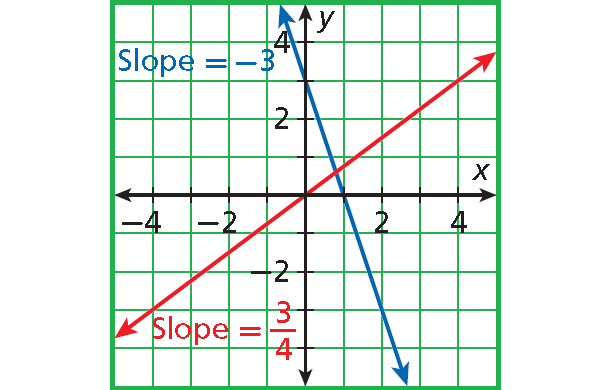
Solution : 

The line with slope -3 is steeper than the line with slope 3/4.

|-3| > |3/4|

Example 4 :

The graph of a line in the xy-plane has slope 1/3 and contains the point (9, 1). The graph of a second line passes through the points (-2, 4) and (5, -3). If the two lines intersect at (a, b), what is the value of a + b ?

a)  -2    b)  2    c) 4      d)  4

Solution :

Equation of the line which has slope 1/3 and containing the point (9, 1).

y - y₁ = m(x - x₁)

y - 1 = (1/3)(x - 9)

3(y - 1) = x - 9

3y - 3 = x - 9

x - 3y - 9 + 3 = 0

x - 3y = 6 -------(1)

Slope of the line containing two points (-2, 4) and (5, -3)

slope (m) = (-3 - 4) / (5 + 2)

= -7/7

m = -1

Equation of the line :

y - y₁ = m(x - x₁)

y - 4 = -1(x + 2)

y - 4 = -x - 2

x + y - 4 + 2 = 0

x + y = 2 -----(2)

(1) - (2)

x - 3y - (x + y) = 6 - 2

-3y - y = 4

-4y = 4

y = -1

Applying the value of y in (1), we get

x - 3(-1) = 6

x + 3 = 6

x = 6 - 3

x = 3

So, the point of intersection is (3, -1).

a = 3 and b = -1

a + b = 3 - 1 ==> 2

So, the value of a + b is 2.

Example 5 :

The line shown in the graph could be the graph of which equation ?

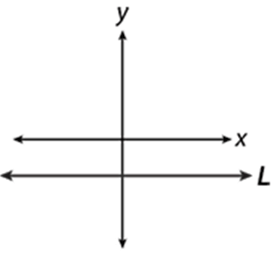
a)  x + y = -2       b)  x + y = 0      c)  x + y - 2 = x

d)  x + y + 2 = x

Solution :

The slope given above is the horizontal line, the slope of a horizontal line will be 0. Equation of horizontal line will be in the form y = k.

In option d,

x + y + 2 = x

x - x + y + 2 = 0

y = -2

So, option d is correct.

Example 6 :

Line l in the -xy plane contains points from each of the Quadrants I, III, and IV, but no points from Quadrant II. Which of the following must be true?

A) The slope of line l is zero.

B) The slope of line l is undefined.

C) The slope of line l is positive.

D) The slope of line l is negative.

Solution :

Some of the lines which lies in the first, third and fourth quadrant.

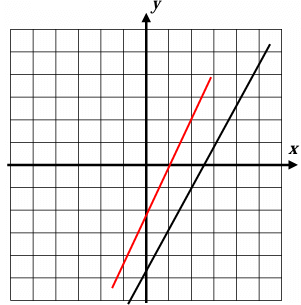
It must be raising line, it has positive slope. So, option C is correct.

Example 7 :

Which of the following lists correctly orders the lines in the figure above according to their slopes, from least to greatest ?

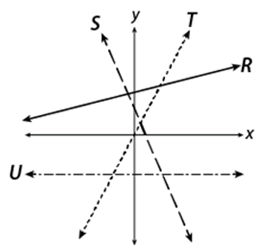
A)  R, T, S, U    B)  S, U, R, T      C) S, R, U, T

D)  U, S, R, T

Solution :

Slope of line R  :

Raising line, will have positive slope.

Slope of line T :

Raising line, will have positive slope.

Slope of line S :

Falling line, will have negative slope

Slope of line U :

Horizontal line, will have no slope.

R, T, S and U. Option a is correct.

Example 8 :

In the x-y plane, the lines y = 2x−1 and y = x+c intersect at point P, where c is a positive number. Portions of these lines are shown in the figure above. If the value of c is between 1 and 2, what is one possible value of the x-coordinate of P ?

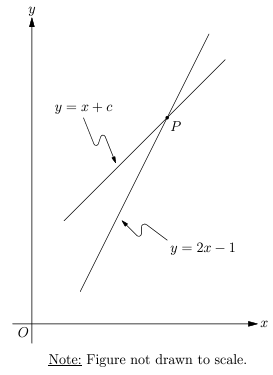
a)  2 < x < 3    b)  5 < x < 7       c)  11 < x < 12 

d) 3 < x < 4

Solution :

As given, y = x + c, y = 2 x − 1

To determine at what point the two lines intersect, set the equations of the lines equal to one another.

x + c = 2x − 1

So, x=c+1 it represents the the x-coordinate of P, the point where the two lines intersect.

Now as per question, if C is between 1 and 2, then the C+1 will be in between 2 and 3. Therefore, the one possible value of the x-coordinate of P can be any value between 2 and 3. Hence, option A is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.