CONGRUENT CHORDS AND ARCS WORKSHEET

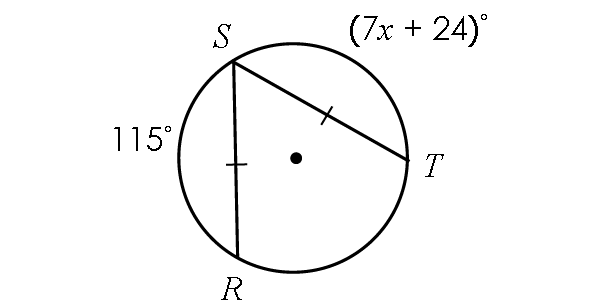
Problem 1 :

Find x. 

Problem 2 :

Find x. 

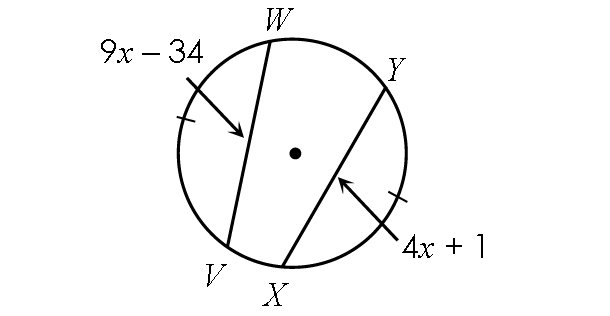
Problem 3 :

Find x. 

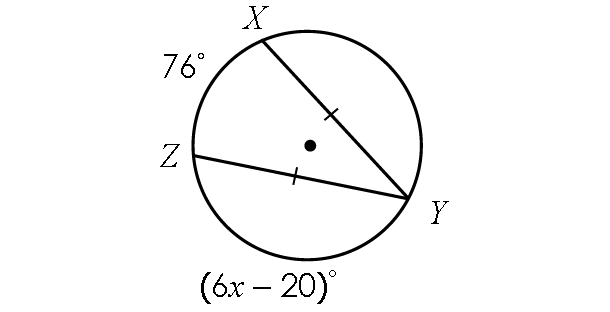
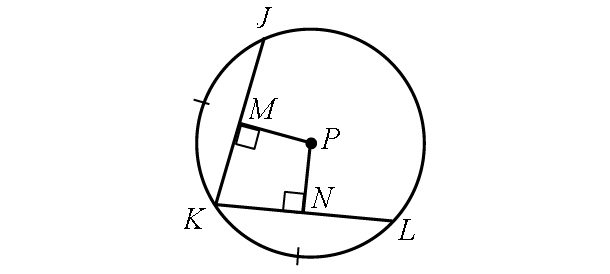
Problem 4 :

If MP = 5x - 34, PN = 2x - 4, find MP.

Problem 5 :

If QM = 6x - 11 and MR = 2x + 9, find MN.

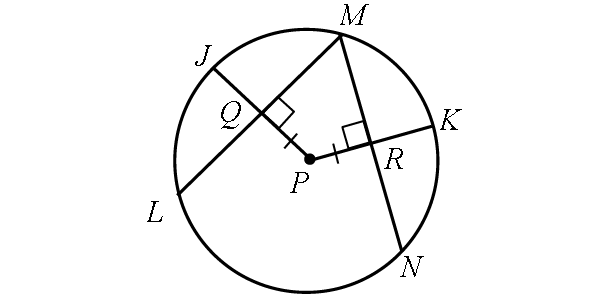
Problem 6 :

In circle Z, if RS = 18, and m∠arcTY = 42°, find the following measures.

(i) TU,  (ii) TU,  (iii) WS,  (iv) m∠arc YU,  (v) m∠arc RS

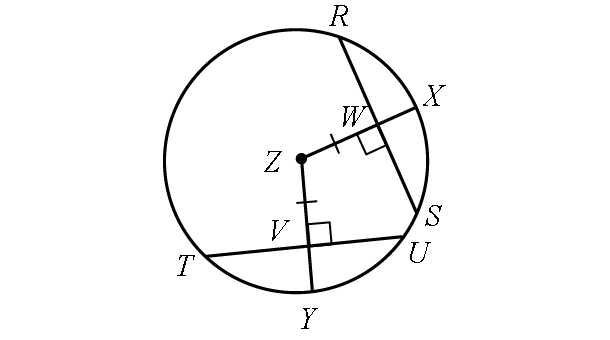
Problem 7 :

Use the circle below to find :

(i) VW  and  (ii) m∠arc YW

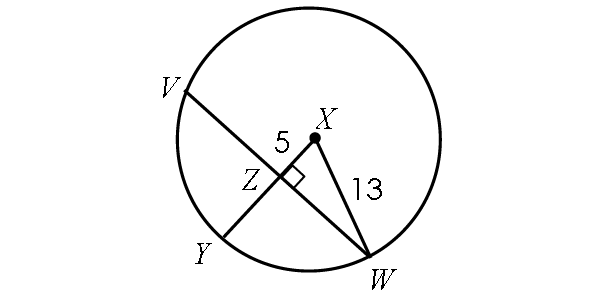
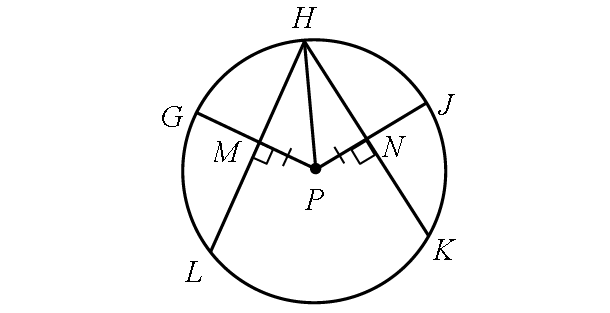
Problem 8 :

In the circle below HK = 30 and PM = 8. Find the following measures : 

(i) PH  and  (ii) m∠arc GJ

Answers

1. Answer :

In the diagram above, the two chords ST and RS are congruent. 

Then, 

ST  =  RS

7x + 24  =  115

Subtract 24 from each side. 

7x  =  91

Divide each side by 7. 

x  =  13

2. Answer :

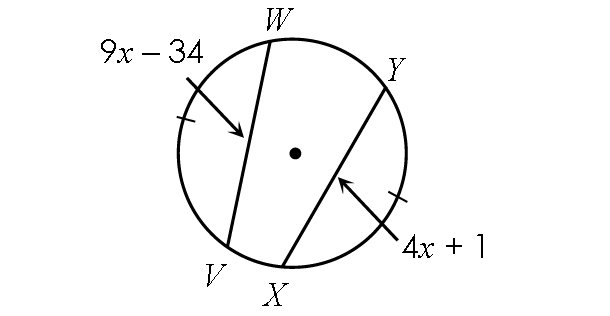
In the diagram above, the two chords VW and XY are congruent. 

Then, 

WV  =  XY

9x - 34  =  4x + 1

Subtract 4x from each side. 

5x - 34  =  1

Add 34 to each side.

5x  =  35

Divide each side by 5. 

x  =  7

3. Answer :

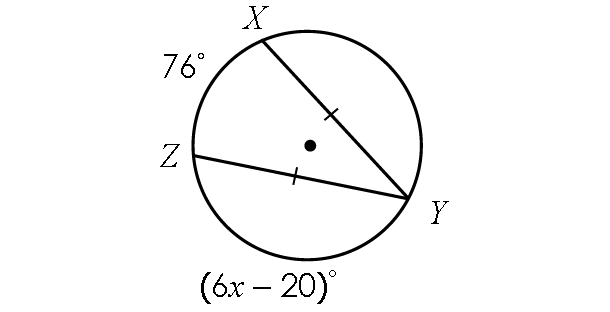
In the diagram above,

m∠arc YZ  =  (6x - 20)°

And also, the two chords YZ and XY are congruent.

Then,

m∠arc XY  =  m∠arc YZ

m∠arc XY  =  (6x - 20)°

In the circle above, 

m∠arc XY + m∠arc YZ + m∠arc ZX  =  360°

(6x - 20)° + (6x - 20)° + 76°  =  360°

6x - 20 + 6x - 20 + 76  =  360

Combine the like terms. 

12x + 36  =  360

Subtract 36 from each side. 

12x  =  324

Divide each side by 12.

x  =  27

4. Answer :

In the diagram above,

m∠arc JK  =  m∠arc KL

Then, the two chords JK and KL are congruent.

Because the two chords JK and KL are congruent, they are equidistant from the center. 

Then, 

MP  =  PN

5x - 34  =  2x - 4

Subtract 2x from each side. 

3x - 34  =  -4

Add 34 to each side. 

3x  =  30

Divide each side by 3. 

x  =  10

Find MP : 

MP  =  5x - 34

Substitute x  =  10. 

MP  =  5(10) - 34

MP  =  50 - 34

MP  =  16

5. Answer :

In the diagram above, the two chords LM and MN are equidistant from the center.

Then, the two chords LM and MN are congruent.

The radii JP and KP are perpendicular to the chords LM and MN respectively.

Then, they bisect the chords. 

Because the chords LM and MN are congruent and they are bisected by the radii, 

QM  =  MR

6x - 11  =  2x + 9

Subtract 2x from each side. 

4x - 11  =  9

Add 11 to each side.

4x  =  20

Divide each side by 4. 

x  =  5

Find MN : 

MN  =  2(MR)

MN  =  2(2x + 9)

MN  =  4x + 18

Substitute x  =  5. 

MN  =  4(5) + 18

MN  =  20 + 18

MN  =  38

6. Answer :

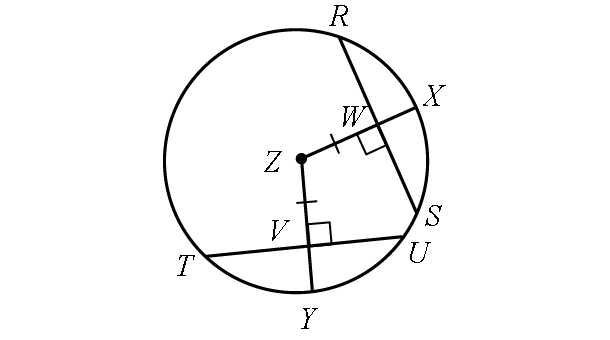
(i) TU : 

Because the two chords RS and TU are equidistant from the center, they are congruent.

TU  =  RS

TU  =  18

(ii) TV : 

Because the radius YZ is perpendicular to the chord TU, the radius YZ bisects the chord TU. 

Then, 

TV  =  TU/2

TV  =  18/2

TV  =  9

(iii) WS : 

Because the radius XZ is perpendicular to the chord RS, the radius XZ bisects the chord RS. 

Then, 

WS  =  RS/2

WS  =  18/2

WS  =  9

(iv) m∠arc YU : 

m∠arc YU  =  m∠arc TY

m∠arc YU  =  42°

(iv) m∠arc RS : 

m∠arc TU  =  m∠arc TY + m∠arc YU

m∠arc TU  =  42° + 42°

m∠arc TU  =  84°

Because the two chords RS and TU are equidistant from the center, they are congruent.

Then, 

m∠arc RS  =  m∠arc TU

m∠arc RS  =  84°

7. Answer :

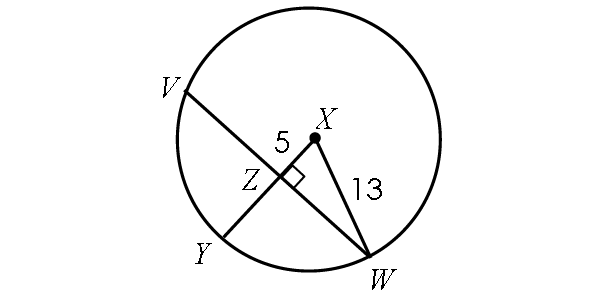
(i) VW : 

Using the Pythagorean theorem in right triangle WXZ,

WZ² + XZ²  =  WX²

WZ² + 5²  =  13²

WZ² + 25  =  169

Subtract 25 from each side. 

WZ²  =  144

WZ²  =  12²

WZ  =  12

Because the radius XY is perpendicular to the chord VW, the radius XY bisects the chord VW. 

Then, 

VW  =  2(WZ)

VW  =  2(12)

VW  =  2

(ii) m∠arc YW : 

In right triangle WXZ, 

cos X  =  5/13

m∠ X  =  cos^-1(5/13)

m∠ X  =  67.4°

Then, 

m∠arc YW  =  67.4°

8. Answer :

(i) PH :

In the circle above,

PN  =  PM

PN  =  8

Because the radius PJ is perpendicular to the chord HK, the radius PJ bisects the chord HK. 

Then,

HN  =  HK/2

HN  =  30/2

HN  =  15

Using the Pythagorean theorem in right triangle HNP,

HN² + PN²  =  PH²

15² + 8²  =  PH²

225 + 64  =  PH²

289  =  PH²

17²  =  PH²

17  =  PH

(ii) m∠arc GJ : 

In right triangle HNP, 

tan P  =  15/8

m∠ P  =  tan^-1(15/8)

m∠ X  =  61.9°

Then, 

m∠arc GJ  =  2 ⋅ m∠ X

m∠arc GJ  =  2 ⋅ 61.9°

m∠arc GJ  =  123.8°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.