CONVERTING BETWEEN MEASUREMENT SYSTEMS

Conversions of units between measurement systems is nothing but converting units from customary to metric system and metric to customary system. 

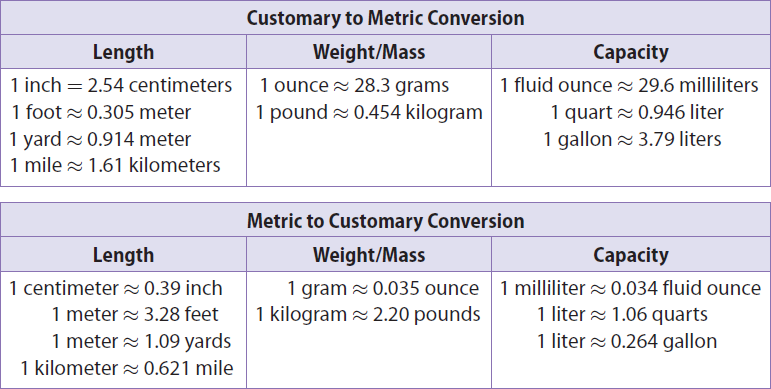
Use the table below to convert units from customary to metric system and metric to customary system. 

Example 1 :

The length of a sheet of paper is 11 inches. What is this length in centimeters ? 

Solution : 

We can use a bar diagram to solve this problem. Each part represents 1 inch.

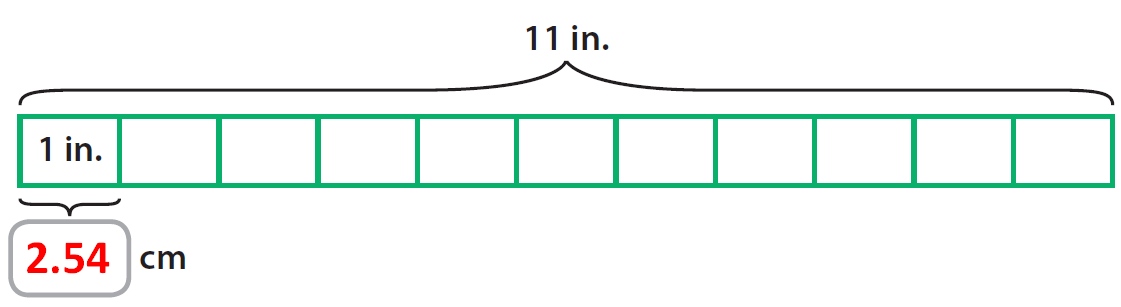
The total length of the above bar diagram is 11 inches and its has been divided into 11 equal parts, each part represents 1 inch

From the above table, in length section of customary to metric conversion, we get

1 inch  ≃  2.54 centimeters

There are eleven 2.54 centimeters in the above bar diagram.  

Then, we have

11 inches  =  11 x 2.54 centimeters

11 inches  =  27.94 centimeters

Another Method :

Another way to solve this problem is to write a proportion and find equivalent ratios.

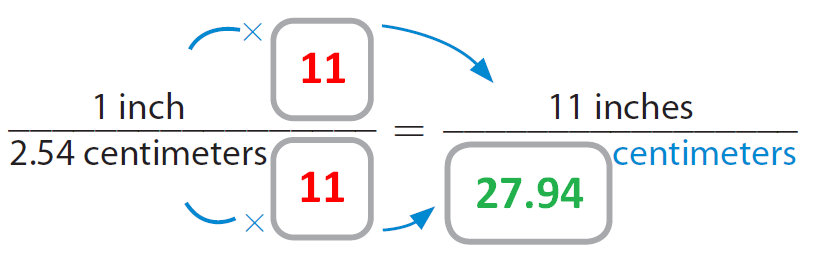
In this method also, we get the same answer. 

That is,

11 inches  =  27.94 centimeters

So, the length of the sheet of paper is 27.94 centimeters approximately.

Example 2 :

Tanya covers 160 miles of distance in 2 hours. Find her speed in kilometer per hour. 

Solution : 

We know the formula for speed.

That is,

Speed  =  Distance / Time

Speed  =  160 miles / 2 hours

Speed  =  80 miles per hour

To find the speed in kilometer per hour, we have to convert 80 miles into kilometers. 

From the above table, in length section of customary to metric conversion, we get

1 miles  ≃  1.61 kilometers

So, we have 

80 miles  =  80 x 1.61 kilometers 

80 miles  =  128.8 kilometers (Approximately)

So, the speed of Tanya is 128.8 kilometers per hour approximately.

Example 3 :

The height of the oak tree is 2.5 meters. What is the height of the oak tree in feet ?

Solution : 

To find the height of the oak tree in feet, we have to convert 2.5 meters into feet. 

From the above table, in length section of metric to customary conversion, we get

So, we have 

1 meter ≃  3.28 feet 

2.5 meters  =  2.5 x 3.28 feet

2.5 meters  =  8.2 feet (Approximately)

So, the height of the oak tree is 8.2 feet approximately.

Example 4 :

Jack ran 4 kilometers each day for 3 days. How many meters did Jack run in 3 days ?

Solution :

Number of kilometers run by Jack = 4 kilometers

Number of days he is running = 3

Number of miles run by Jack = 3(4)

= 12 kilometers

Example 5 :

Bella is 4 feet tall, and her brother is 5 feet tall. How many inches tall are Bella and her brother combined?

Solution :

Height of Bella = 4 feet

Height of her brother = 5 feet

Difference = 5 -4

= 1 feet

So, her brother is 1 feet taller than Bella.

Example 6 :

Kim drank two quarts of juice, and Alice drank two pints of juice. How many cups of juice did they drink altogether?

Solution :

Quantity of juice Kim drank = 2 quarts

Quantity of juice Alice drank = 2 pints

Quantity of juice they drink altogether = 2 quarts + 2 pints

1 quart = 4 pints

2 quart = 2(4)

= 8 pints

= 8 pints + 2 pints

= 10 pints.

So, they together drank 10 pints.

Example 7 :

Melissa's bunny weighs 1,800 grams. How many kilograms does her bunny weigh?

Solution :

Weight of Melissa's bunny = 1800 grams

1 kg = 1000 grams

= 1800/1000

= 1.8 kg

Example 8 :

An elephant can drink 190 liters of water each day. How many milliliters of water could four elephants drink in one day?

Solution :

Example 9 :

Mary drove 24 kilometers to the mall. How many meters will she have driven by the time she returns home?

Solution :

Example 10 :

Joe orders three pizzas that each weigh 900 grams. How many kilograms do all of Joe's pizzas weigh?

Solution :

Weight of each pizza = 900 grams

Weight of three pizzas = 3(900)

= 2700 grams

1 kilogram = 1000 grams

= 2700/1000

= 2.7 kilograms

So, weight of all pizzas is 2.7 kilograms

Example 11 :

Cody’s notebook is 3 centimeters tall, 10 centimeters wide, and 13 centimeters long. What is the volume of Cody’s notebook?

Solution :

Length of notebook = 13 cm

Width = 10 cm

Height = 3 cm

Volume of notebook = length x width x height

= 13 x 10 x 3

= 390 cm³

So, volume of Cody's notebook is 390 cm³.

Example 12 :

Mr. Arthur's cabinet has a height of 6 feet, a width of 4 feet, and a length of 5 feet. What is the volume of Mr. Arthur's cabinet?

Solution :

Length of cabinet = 5 feet

Width = 4 feet

Height = 6 feet

Volume of cabinet = length x width x height

= 5 x 4 x 6

= 120 cubic feet

Example 13 :

Kendra's suitcase is 24 inches tall, 16 inches wide, and 12 inches long. What is the volume of Kendra's suitcase?

Solution :

Length of cabinet = 12 inches

Width = 16 inches

Height = 24 inches

Volume of cabinet = length x width x height

= 12 x 16 x 24

= 4608 cubic inches

Example 14 :

A shipping container is 3 meters tall, 3 meters wide, and 15 meters long. What is the volume of the shipping container?

Solution :

Length of cabinet = 15 meter

Width = 3 meter

Height = 3 meter

Volume of cabinet = length x width x height

= 15 x 3 x 3

= 135 cubic meter

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.