CONVERTING UNITS USING RATIOS AND PROPORTIONS

We can use ratios and proportions to convert both customary and metric units.

Use the table below to convert from one unit to another within the same measurement system.

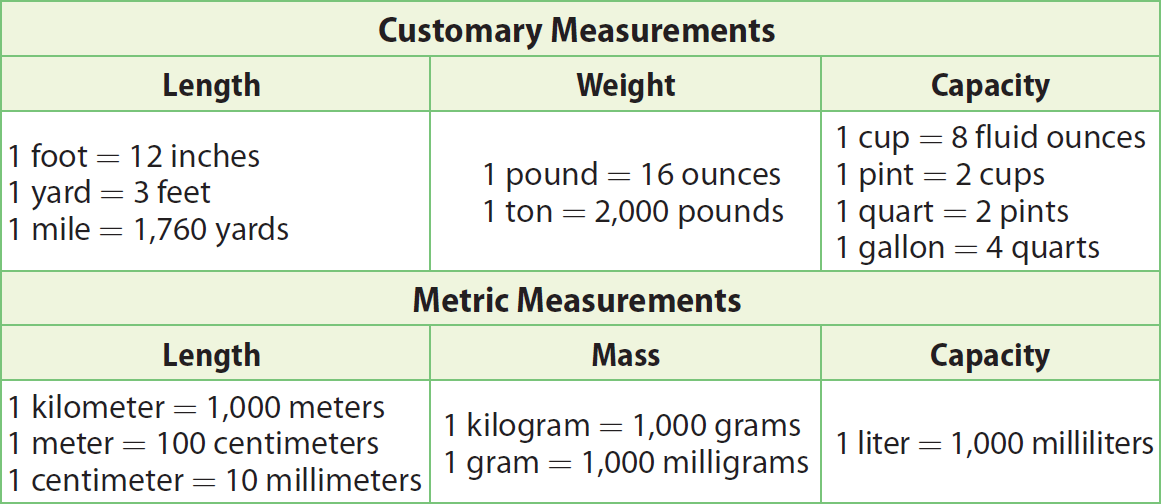
Each relationship in the table can be described by two ratios.

For example, because 1 quart = 2 pints, we can write two ratios 1 quart/2 pints and 2 pints/1 quart.

Problem 1 :

An average human brain weighs 3 pounds. What is this weight in ounces ? Use a proportion to convert 3 pounds to ounces.

Solution :

Step 1 :

Identify the ratio that compares the units involved.

The units pounds and ounces are customary units of weight.

Find the relationship of those units in the weight section of the customary measurements table.

1 pound = 16 ounces

Step 2 :

Write a proportion.

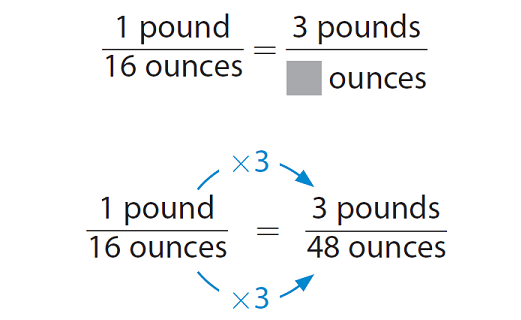
Because 1 x 3  =  3, multiply 16 by 3.

A weight of 3 pounds is equal to 48 ounces.

Problem 2 :

A moderate amount of daily sodium consumption is 2,000 milligrams. What is this mass in grams ? Use a proportion to convert 2,000 milligrams to grams.

Solution :

Step 1 :

Identify the ratio that compares the units involved.

The units, milligrams and grams, are metric units of mass.

Find the relationship of those units in the mass section of the metric measurements table :

1 gram = 1,000 milligrams

Step 2 :

Write a proportion.

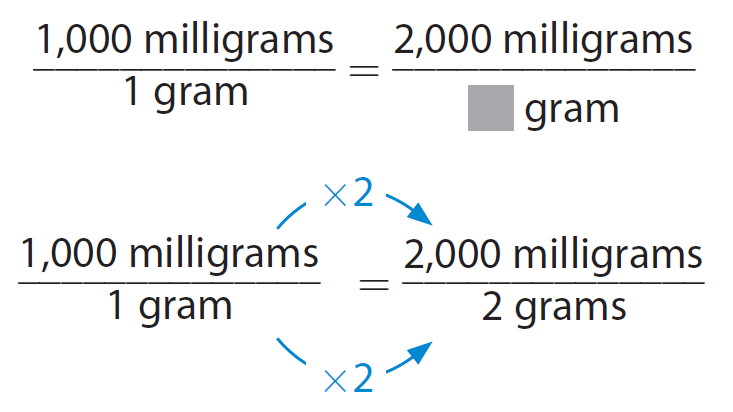
Because 1000 x 2 = 2000, multiply 1 by 2.

A mass of 2,000 milligrams is equal to 2 grams.

Problem 3 :

The height of a doorway is 6 feet. What is the height of the doorway in inches?

Solution :

Step 1 :

Identify the ratio that compares the units involved.

The units feet and inches are customary units of length.

Find the relationship of those units in the length section of the customary measurements table :

1 foot = 12 inches

Step 2 :

Write a proportion.

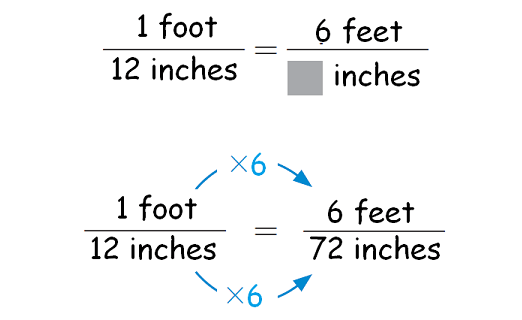
Because 1 x 6 = 6, multiply 12 by 6.

A length of 6 feet is equal to 72 inches.

Problem 4 :

According to the American Automobile Association (AAA), the overall cost of owning an operating a passenger vehicle averages $7834 based on 15000 miles of driving. If the cost per mile is constant, about what would it cost to drive 12000 miles ?

Solution :

Here cost of the vehicle is compared with number of miles driving.

Let x be the cost of vehicle to drive 12000 miles.

7834 : 15000 = x : 12000

7834/15000 = x/12000

x = 7834(12000)/15000

= 6267.2

So, the required cost is $6267.2

Problem 5 :

A typical scale for a house plan is 1/4 inch to 1 foot. If the width of the room on such plan measures 3  1/2 inches, what is the actual width of the room ?

Solution :

1/4 inch : 1 foot

Let x be the actual width of the room in foot.

1/4 : 1 = 3  1/2 : x

1/4 / 1 = 7/2 : x

1/4 = 7/2x

2x = 7(4)

2x = 28

x = 14

So, the actual width of the room is 14 foot.

Problem 6 :

Walking at fast pace burns 5.6 calories per minute. How many minutes of walking at the fast pace are needed to burn the 500 calories consumed by eating a dish of ice cream ?

Solution :

Amount of calories burns is compared with time of walking.

Let x be the needful time.

5.6 : 1 = 500 : x

5.6/1 = 500/x

x = 500/5.6

x = 89 minutes (approximately)

So, to burn 500 calories he has to walk 1 hour and 39 minutes in the fast pace.

Problem 7 :

The ratio of the corresponding sides of two similar rectangles is 4 : 9. If the length of the smaller rectangle is 16 cm and its width is 12 cm. What is the perimeter of the larger rectangle ?

Solution :

Scale factor for smaller rectangle to larger rectangle

= 4 : 9

Length of the smaller rectangle = 16 cm

Let x be the length of the larger rectangle.

4 : 9 = 16 : x

4/9 = 16/x

x = 16(9)/4

x = 36 cm

Let y be the width of the larger rectangle

4 : 9 = 12 : y

4/9 = 12/y

y = 12(9)/4

y = 27 cm

Perimeter of larger rectangle 

= 2(36 + 27)

= 2(63)

= 126 cm

Problem 8 :

A model length of 12 cm represents an actual length of 102 ft. What is the scale for the model ?

Solution :

Length in model = 12 cm

Actual length = 102 ft

Scale = 12 : 102

= 12/102

= 4/34

= 2 : 17

Problem 9 :

Jenny can type 1200 words in just 15 minutes. How many words can she type in an hour ?

Solution :

Ratio between number of words she is typing and time taken in minutes = 1200 : 15

1 hour = 60 minutes

Let x be the number of words she is typing for 60 minutes

1200 : 15 = x : 60

1200/15 = x/60

x = (1200/15) ⋅ 60

= 1200 ⋅ 4

= 4800

So, the required number of words is 4800.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.