CURVED SURFACE AREA AND TOTAL SURFACE AREA OF SPHERE AND HEMISPHERE

Curved Surface Area and Total Surface Area of Hemisphere

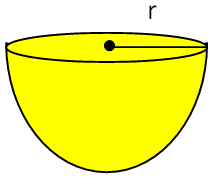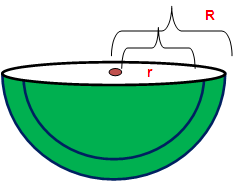Curved surface area  =  2Πr2 Hollow hemisphere = 2Π(R2 + r2) sq. units Total surface area of  =  3Πr2 Hollow hemisphere  =  Π(3R2 + r2) sq. units

Problem 1 :

The radius of a sphere increases by 25%. Find the percentage increase in its surface area.

Solution :

Radius of hemisphere  =  r

Increased percentage of radius  =  125% of r

  =  125r/100

  =  5r/4

Surface area of hemisphere   =  2Πr²

Surface area of increased hemisphere   =  2Π(5r/4)²

  =  25Πr²/8

  =  [(25Πr²/8) - (2Πr²)]/(2Πr²)

  =  9Πr²/8(2Πr²)

  =  9Πr²/16 Πr²

  =  0.5625

  =  0.5625 (100)

  =  56.25%

Problem 2 :

The internal and external diameters of a hollow hemispherical vessel are 20 cm and 28 cm respectively. Find the cost to paint the vessel all over at ₹0.14 per cm² 

Solution :

internal radius (r)  =  20/2  =  10 cm

External radius (R) =  28/2  =  14 cm

Curved surface area of hemisphere  = 2Π(R² + r²) 

  =  2 (22/7)(14² + 10²)

  =  2 (22/7)(196 + 100)

  =  1860.57

Cost of painting  =  ₹0.14 per cm² 

Required cost  =  0.14 (1860.57)

  =  ₹260.48 

Problem 3 :

What will be the diameter of a sphere whose surface area is 55.44 m²?

(a) 4.6 m (b) 4.2 m (c) 3.4 m (d) 2.4 m

Solution :

Surface area of sphere = 4Πr²

4Πr² = 55.44

4 x (22/7) x r² = 55.44

r² = 55.44 x (1/4) x (7/22)

r² = 4.41

r = √4.41

r = 2.1

Diameter = 2r

= 2 (2.1)

= 4.2 m

So, the required diameter is 4.2 m.

Problem 4 :

The curved surface area of a sphere of radius 7 cm is

Solution :

Curved surface area of the sphere = 4Πr²

Here radius (r) = 7 cm

= 4 x (22/7) x 7 x 7

= 616 cm²

Problem 5 :

Find the total surface area of a hemisphere of radius r/2 unit

Solution :

Total surface area of hemisphere = 3Πr²

radius = r/2

= 3 x Π x (r/2)²

= 3 x Π x (r²/4)

= (3/4) Π r² 

Problem 6 :

The radius of a spherical balloon increases from 7 cm to 14 cm when air is being pumped into it. Then find the ratio of surface area of the balloon in the two cases.

Solution :

Old radius = 7 cm and new radius = 14 cm

Surface area of balloon = 4Πr²

Let old radius be r and new radius be R.

= 4ΠR² : 4Πr²

= 4Π(14)² : 4Π(7)²

= (14)² : (7)²

= 4 : 1

So, the required ratio is 4 : 1.

Problem 7 :

A cylinder, a cone and a sphere are of the same radius and same height. Find the ratio of their curved surface.

Solution :

Radius of cylinder = radius of cone = radius of sphere = r = h

Surface area of cylinder = 2Πrh

Surface area of sphere = 4Πr²

Surface area of cone = Πrl

l = √r² + h²

l = √r² + r²

l = √2r²

l = r√2

Surface area of cylinder : Surface area of cone : Surface area of sphere

= 2Πrh : Πrl : 4Πr²

= 2r(r) : r (r√2) : 4r²

= 2r² : r²√2 : 4r²

= 2 : √2 : 4

= 1 : √2 : 2

= 1 : 2 : 4

So, the required ratio is 1 : 2 : 4.

Problem 8 :

Find the radius of a sphere with a surface area of 1024π square inches.

Solution :

Surface area of sphere = 4Πr²

1024π = 4Πr²

1024 = 4r²

r² = 1024/4

r² = 256

r = 16

So, the radius of the sphere is 16 inches.

Problem 9 :

You friend claims that if the radius of a sphere is doubled, then the surface area of the sphere will also be doubled. Is your friend correct? Explain your reasoning.

Solution :

Let radius of the sphere be r, then when it is double the new radius will be 2r.

Surface area of sphere = 4Πr²

When r = 2r

Surface area of new sphere = 4Π(2r)²

= 16Πr²

= 4 (4Πr²)

= 4(surface area of old sphere)

So, it is incorrect.

Curved Surface Area and Total Surface Area of Frustum Cone

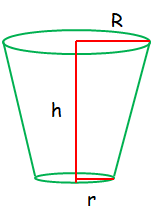C.S.A. of a frustum   =  Π(R +r)l sq. units T.S.A. of a frustum   =  Π(R + r)l + Π(R2+ r2) where, l = √[h2 +(R −r)2]

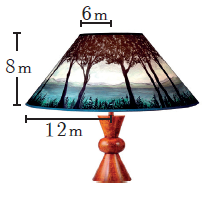
Problem 10 :

Th e frustum shaped outer portion of the table lamp has to be painted including the top part. Find the total cost of painting the lamp if the cost of painting 1 sq.cm is ₹2.

Solution :

Curved surface area of lamp  =  Π(R +r)l sq. units

R = 12 m, r = 6 m and h = 8 m

l = √[h² +(R −r)²]

l = √[8² +(12 −6)²]

l = √[64 + 6²]

l = √(64 + 36)  = √100

l = 10

C.S.A of frustum shaped lamp  =  Π(R +r)l 

Area to be painted  =  Π(R +r)l + Πr²

  =  (22/7)[(12 + 6)(10) + 6²]

=  (22/7)[180+36]

=  678.85

Cost per sq.cm is ₹2

Required cost  =  678.85 (2)

  =  ₹1357.71

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.