DEFINITION OF BINOMIAL

What if two terms are in multiplication or division?

An algebraic expression in which two terms are in multiplication or division is not binomial.

For example, x²y is not a binomial. Even though we have two terms x² and y in x²y,  we can not consider x²y as binomial. Because x² and y are in multiplication.

Algebraic Identities of Binomials

(a + b)² = a² + 2ab + b²

(a - b)² = a² - 2ab + b²

a² - b² = (a + b)(a - b)

(a + b)³ = a³ + 3a²b + 3ab² + b³

or

= a³ + 3ab(a + b) + b³

(a - b)³ = a³ - 3a²b + 3ab² - b³

or

= a³ - 3ab(a - b) - b³

a³ + b³ = (a + b)³ - 3ab(a + b)²

a³ - b³ = (a - b)³ + 3ab(a - b)²

Adding Binomials

To add two or more binomials, we have to group the like terms and combine them.

Example 1 :

Simplify :

(x + y) + (2x - 3y)

Solution :

= (x + y) + (2x - 3y)

= x + y + 2x - 3y

Group the like terms and combine them.

= (x + 2x) + (y - 3y)

= 3x + (-2y)

= 3x - 2y

Example 2 :

Simplify :

(5x²y + 3) + (5 - 3x²y)

Solution :

= (5x²y + 3) + (5 - 3x²y)

= 5x²y + 3 + 5 - 3x²y

Group the like terms and combine them.

= (5x²y - 3x²y) + (3 + 5)

= 2x²y + 8

Example 3 :

Simplify :

(3xy + 3) + (5x + xy)

Solution :

= (3xy + 3) + (5x + xy)

= 3xy + 3 + 5x + xy

Group the like terms and combine them.

= (3xy + xy) + 5x + 3

= 4xy + 5x + 3

Example 4 :

Simplify :

(x² + 3xy²) + (5x² - 3x²y) + (7xy² - 5x²y)

Solution :

= (x² + 3xy²) + (5x² - 3x²y) + (7xy² - 5x²y)

= x² + 3xy² + 5x² - 3x²y + 7xy² - 5x²y

Group the like terms and combine them.

= (x² + 5x²) + (-3x²y - 5x²y) + (3xy² + 7xy²)

= 6x² + (-8x²y) + 10xy²

= 6x² - 8x²y + 10xy²

Subtracting Binomials

To subtract two binomials, distribute the negative sign to the terms in the second binomial and group the like terms and combine them.

Example 5 :

Simplify :

(a + 2b) - (2a + b)

Solution :

= (a + 2b) - (2a + b)

Distribute the negative sign.

= a + 2b - 2a - b

Combine the like terms by grouping.

= (a - 2a) + (2b - b)

= -a + b

= b - a

Example 6 :

Simplify :

(7pq + 4) - (3p - 5pq)

Solution :

= (7pq + 4) - (3p - 5pq)

Distribute the negative sign.

= 7pq + 4 - 3p + 5pq

Combine the like terms by grouping.

= (7pq + 5pq) - 3p + 4

= 12pq - 3p + 4

Example 7 :

Simplify :

(7xy² + 5) - (3 + 2xy²)

Solution :

= (7xy² + 5) - (3 + 2xy²)

Distribute the negative sign.

= 7xy² + 5 - 3 - 2xy²

Combine the like terms by grouping.

= (7xy² - 2xy²) + (5 - 3)

= 5xy² + 2

Example 8 :

Simplify :

(3x² - 5x²y) - (2x²y - 7x²)

Solution :

= (3x² - 5x²y) - (2x²y - 7x²)

Distribute the negative sign.

= 3x² - 5x²y - 2x²y + 7x²

Combine the like terms by grouping.

= (3x² + 7x²) + (-5x²y - 2x²y)

= 10x² + (-7x²y)

= 10x² - 7x²y

Multiplying Binomials

You can use the following methods to multiply a binomial by a binomial.

(i) Distributive Property.

(ii) FOIL Method

Distributive Property

To multiply a binomial by a binomial, Distributive Property can be used more than once.  

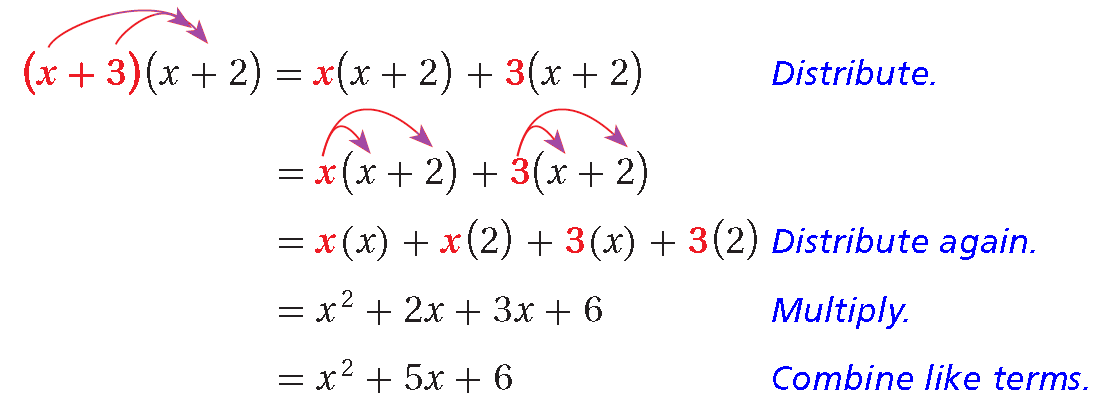
FOIL Method

Another method for multiplying binomials is called the FOIL method. 

1. Multiply the First terms.

2. Multiply the Outer terms.

3. Multiply the Inner terms.

4. Multiply the Last terms.

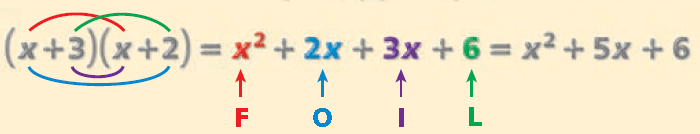
Example 9 : 

Multiply using Distributive Property. 

(p + 2)(p - 5)

Solution :

= (p + 2)(p - 5)

Distribute. 

= p(p - 5) + 2(p - 5)

Distribute again. 

= p² - 5p + 2p - 10

Combine the like terms.

= p² - 3p - 10

Example 10 : 

Expand (x + y)² using Distributive Property.

Solution :

= (x + y)²

Write as a product of two binomials.

= (x + y)(x + y)

Distribute.

= x(x + y) + x(x + y)

Distribute again. 

= x² + xy + xy + y²

Combine the like terms.

=  x² + 2xy + y²

Example 11 : 

Multiply using FOIL method. 

(5x² - 2y)(x² + 3y)

Solution :

= (5x² - 2y)(x² + 3y)

Use the FOIL method. 

= (5x² ⋅ x²) + (5x²⋅ 3y) + (-2y ⋅ x²) + (-2y ⋅ 3y)

Multiply.

= 5x⁴ + 15x²y + (-2x²y) + (-6y²)

= 5x⁴ + 15x²y - 2x²y - 6y²

Combine the like terms. 

= 5x⁴ + 13x²y - 6y²

Example 12 : 

Expand (y - 3)² using FOIL method.

Solution :

= (y - 3)²

Write as a product of two binomials. 

= (y - 3)(y - 3)

Use the FOIL method. 

= (y ⋅ y) + (y ⋅ -3) + (-3 ⋅ y) + (-3 ⋅ -3)

Multiply. 

= y² + (-3y) + (-3y) + 9

= y² - 3y - 3y + 9

Combine like terms. 

= y² - 6y + 9

Practice Questions

Click here to get detailed answers for the above questions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.