DERIVATIVES OF INVERSE FUNCTIONS

Conider a function f(x). Let g(x) be the inverse function of f(x). That is,

g(x) = f^-1(x)

Take the function f on both sides using the operation function composition.

f ∘ g(x)] = f ∘ f^-1(x)

f[g(x)] = f[f^-1(x)]

f[g(x)] = f^1-1(x)

f[g(x)] = f⁰(x)

f[g(x)] = x

Find the derivative on both sides with respect to x. (Use chain rule on the left side. That is, first find the derivative of f, then by chain rule, find the derivative of g(x)).

f'[g(x)] ⋅ g'(x) = 1

Divide both sides by f'[g(x)].

Replace g(x) by f^-1(x).

Let g(2) = k.

Since g(x) is the inverse of f(x),

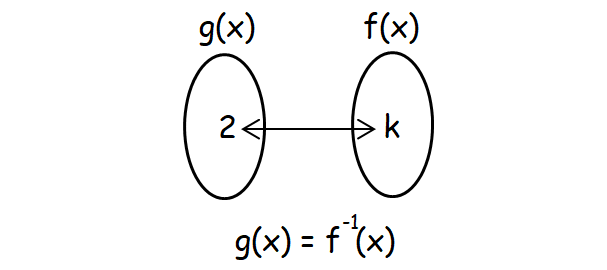
Therefore,

f(k) = 2

2k + 1 = 2

Subtract 1 from both sides.

2k = 1

Divide both sides by 2.

k = ½

Since g(2) = k,

g(2) = ½

f(x) = 2x + 1

f'(x) = 2(1) + 0

f'(x) = 2

Substitute x = ½.

f'(½) = 2

Let g(5) = k.

Since g(x) is the inverse of f(x),

f(k) = 5

k³ + k + 5 = 5

Subtract 5 from both sides.

k³ + k = 0

k(k² + 1) = 0

Therefore,

k = 0

Since g(5) =k,

g(5) = 0

f(x) = x³ + x + 5

f'(x) = 3x² + 1

Substitute x = 0.

f'(0) = 3(0)² + 1

f'(0) = 0 + 1

f'(0) = 1

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

About Us  |  Contact Us  |  Privacy Policy

©All rights reserved. onlinemath4all.com