DETERMINE IF THE RELATIONSHIP IS PROPORTIONAL WORKSHEET

Problem 1 : 

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

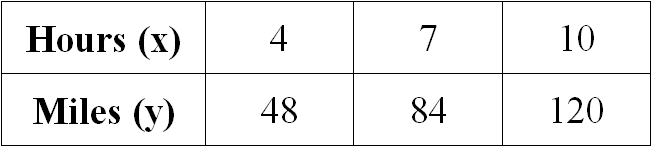
Problem 2 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

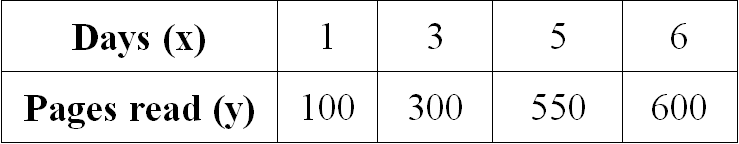
Problem 3 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

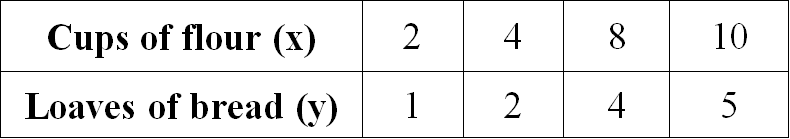
Problem 4 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

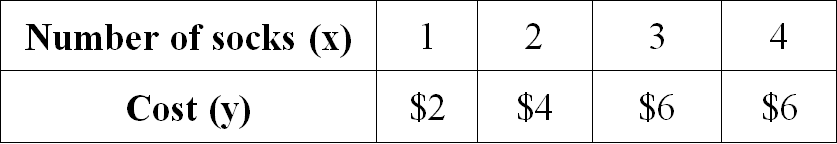
Problem 5 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

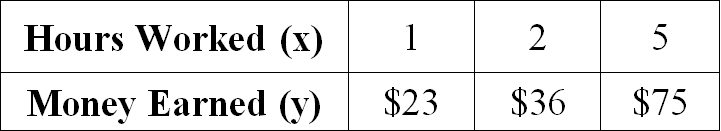
Problem 6 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality.

1. Answer :

Let us get the ratio of x and y for all the given values.

4/48 = 1/12

7/84 = 1/12

10/120 = 1/12

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx

Substitute x = 4 and y = 48.

48 = k(4)

12 = k

So, the constant of proportionality is 12.

2. Answer :

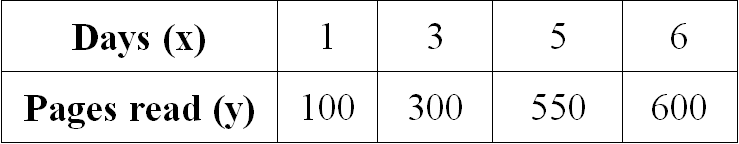
Let us get the ratio of x and y for all the given values.

1/100 = 1/100

3/300 = 1/100

5/550 = 1/110

6/600 = 1/100

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

Therefore the relationship given in the table is not proportional.

3. Answer :

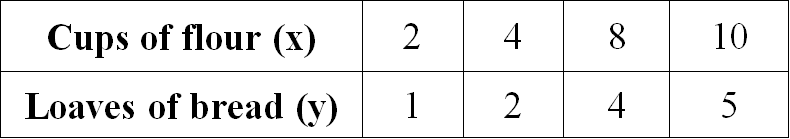
Find the ratio of x and y for all the given values.

2/1 = 2

4/2 = 2

8/4 = 2

10/5 = 2

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore, the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx 

Substitute 2 for x and 1 for y.

1 = k(2)

1/2 = k

So, the constant of proportionality is 1/2.

4. Answer :

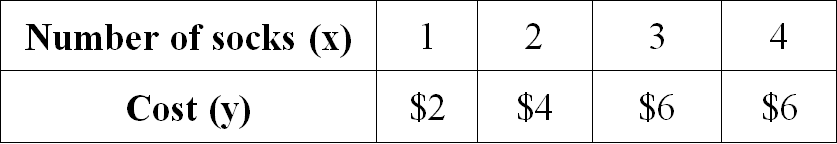
Let us get the ratio of x and y for all the given values.

1/2 = 1/2

2/4 = 1/2

3/6 = 1/2

4/6 = 2/3

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

Therefore the relationship given in the table is not proportional.

5. Answer :

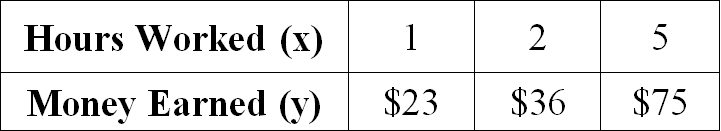
Let us get the ratio of x and y for all the given values.

1/23 = 1/23

2/36 = 1/18

5/75 = 1/15

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

Therefore the relationship given in the table is not proportional.

6. Answer :

Let us get the ratio of x and y for all the given values.

2/4 = 1/2

4/8 = 1/2

6/12 = 1/2

8/16 = 1/2

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore the relationship given in the table is proportional.

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion.

Then, we have

y = kx

Substitute x = 2 and y = 4.

4 = k(2)

2 = k

So, the constant of proportionality is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.