DIFFERENCE BETWEEN COMPOUND AND SIMPLE INTEREST FOR 3 YEARS

The formula given below can be used to find the difference between compound interest and simple interest for three years.

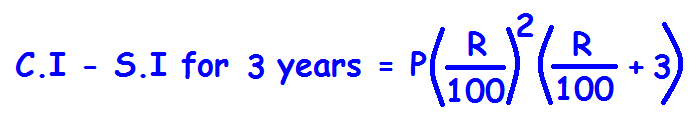
The above formula is applicable only in the following conditions.

1. The principal in simple interest and compound interest must be same.

2. Rate of interest must be same in simple interest and compound interest.

3. In compound interest, interest has to be compounded annually.

Example 1 :

$800 is invested in both simple interest and compound interest at the same rate of interest for three years. If the rate of interest is 20%, find the difference between compound interest and simple interest.

Solution :

The formula for difference between compound interest and simple interest for three years is

C.I - S.I = P(R/100)²(R/100 + 3)

In the above formula, substitute R = 20, P = 800.

C.I - S.I = 800(20/100)²(20/100 + 3)

Simplify

C.I - S.I = 800(1/5)²(1/5 + 3)

= 800(1/25)(16//5)

= 800 x 16/125

= 800 x 16/125

= 102.40

So, the difference between compound interest and simple interest is $102.40.

Example 2 :

The difference between the compound interest and simple interest on a certain principal is at 10% per year for 3 years is $31. Find the principal.

Solution :

The difference between compound interest and simple interest for three years is 31.

Then we have,

P(R/100)²(R/100 + 3) = 31

Substitute R = 10.

P(10/100)²(10/100 + 3) = 31

P(1/10)²(1/10 + 3) = 31 

P(1/10)²(31/10) = 31

P(1/100)(31/10) = 31

P(31/1000) = 31

Multiply both sides by 1000/31.

P = 31 x (1000/31)

P = 1000

So, the principal is $1000.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.