DIRECT VARIATION WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1-3 : Tell whether each equation represents a direct variation. If so, identify the constant of variation.
Problem 1 :
y = 4x
Problem 2 :
-2x + 3y = 0
Problem 3 :
3x + 2y = 6
Problem 4-7 : Tell whether each relationship is a direct variation. Explain.
Problem 4 :

Problem 5 :

Problem 6 :

Problem 7 :

Problem 8 :
The value of y varies directly with x, and y = 8 when x = 2. Find y when x = 5.
Problem 9 :
The value of y varies directly with x, and y = 4.5 when x = 0.5. Find y when x = 10.
Problem 10 :
The three-toed sloth is an extremely slow animal. On the ground, it travels at a speed of about 6 feet per minute. Write a direct variation equation for the distance y a sloth will travel in x minutes. Then graph.

1. Answer :
This equation represents a direct variation, because it is in the form y = kx. The constant of variation is 4.
2. Answer :
-2x + 3y = 0
Solve the equation for y.
Because -2x is added to 3y, add 2x to each side.
3y = 2x
Because y is multiplied by 3, divide each side by 3.
3y/3 = 2x/3
y = (2/3)x
This equation represents a direct variation, because it can be written in the form y = kx. The constant of variation is 2/3.
3. Answer :
3x + 2y = 6
Solve the equation for y.
Because 3x is added to 2y, subtract 3x from each side.
2y = -3x + 6
Because y is multiplied by 2, divide each side by 2.
2y/2 = (-3x + 6)/2
y = -3x/2 + 6/2
y = -3x/2 + 3
This equation does not represent a direct variation, because it cannot be written in the form y = kx.
4. Answer :
Write an equation that represents the relationship given in the table above.
y = 6x
Each y-value is 6 times the corresponding x-value.
This is a direct variation.
Because the equation y = 6x is in the form of y = kx, where k = 6.
5. Answer :
Write an equation that represents the relationship given in the table above.
y = x - 4
Each y-value is 4 less than the corresponding x-value.
This is a not direct variation.
Because the equation y = x - 1 is not in the form of y = kx.
6. Answer :
Write an equation that represents the relationship given in the table above.
y = -4x
Each y-value is -4 times the corresponding x-value.
This is a direct variation.
Because the equation y = -4x is not in the form of y = kx, where k = -4.
7. Answer :
From the table, we have the following ordered pairs.
(-2, 5), (1, 3) and (4, 1)
Plotting the above points in xy-plane, we get a straight line with slope -2/3 and y-intercept 11/3
So, the equation is
y = -2x/3 + 11/3
This is not a direct variation.
Because the above equation is not in the form of y = kx.
8. Answer :
It is given that y varies directly with x.
Write the equation for a direct variation.
y = kx
Substitute 8 for y and 2 for x.
8 = k(2)
8 = 2k
Divide each side by 2.
8/2 = 2k/2
4 = k
The equation is
y = 4x
Find y, when x = 5.
y = 4(5)
y = 20
9. Answer :
It is given that y varies directly with x.
Write the equation for a direct variation.
y = kx
Substitute 4.5 for y and 0.5 for x.
4.5 = k(0.5)
4.5 = 0.5k
Divide each side by 0.5.
4.5/0.5 = 0.5k/0.5
9 = k
The equation is
y = 9x
Find y, when x = 10.
y = 9(10)
y = 90
10. Answer :
Step 1 :
Write a direct variation equation.
Distance
is
6 feet per minute
times
number of minutes
y
=
6
⋅
x
Step 2 :
Choose values of x and generate ordered pairs.
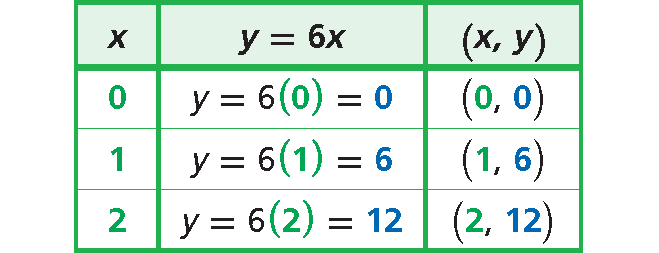
Step 3 :
Graph the points and connect.
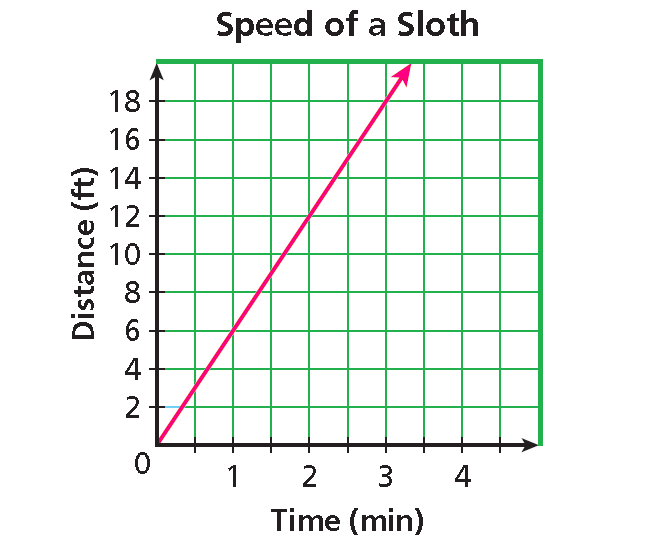
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37) -
Factorial Problems and Solutions
Dec 02, 25 09:27 AM
Factorial Problems and Solutions

