DOMAIN AND RANGE OF A RELATION WORKSHEET

Problem 1 : 

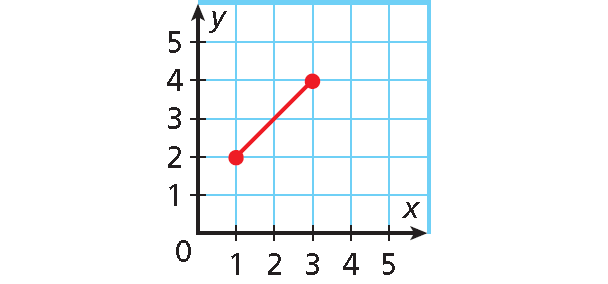
Find the domain and range of the relation shown in the graph below. 

Problem 2 :

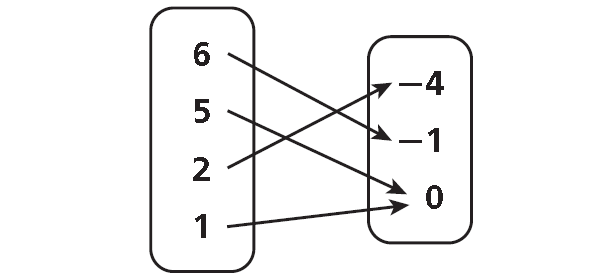
Find the domain and range of the relation shown in the mapping diagram below. 

Problem 3 :

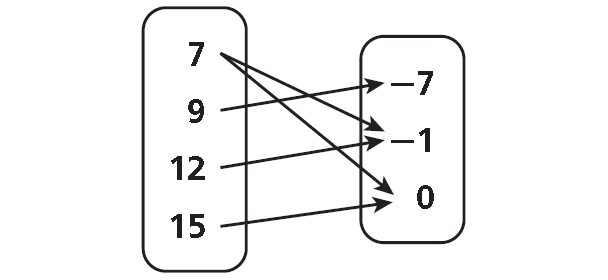
Find the domain and range of the relation shown in the mapping diagram below. 

Problem 4 :

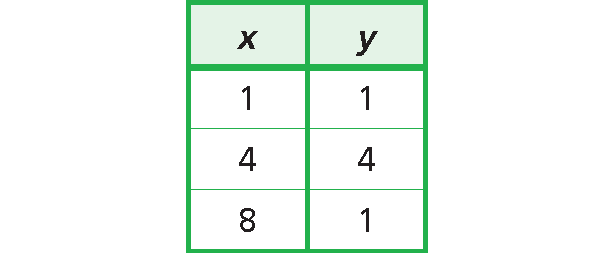
Find the domain and range of the relation shown in the table below. 

Problem 5 :

Let A = {1, 2, 3, 4} and B = {1, 4, 9, 16, 25}. If R is the relation which maps the elements from A to B using the rule f(x) = x², then find the domain and range of R. 

Problem 6 : 

Let A  =  {1, 2, 3} and B  =  {5, 6, 7, 8}. 

R is the relation which maps the elements from A to B as shown below. 

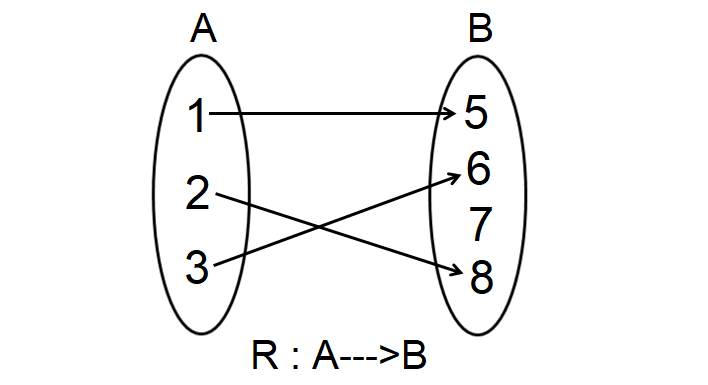
Find the domain and range of R.

Problem 7 : 

Let X  =  {a, b, c} and Y  =  {d, e, f, g}. 

R is the relation which maps the elements from X to Y as shown below. 

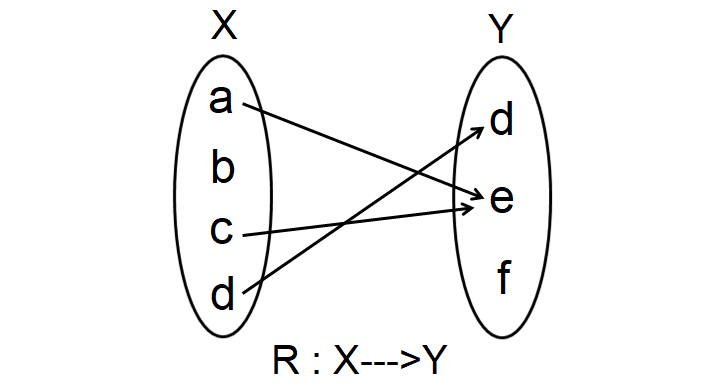
Find the domain and range of R.

Problem 8 : 

Let R be a relation defined as given below.  

R  =  {(1, 1), (2, 3), (3, 4), (2, 7)}

Find the domain and range of R and R^-1. Discuss the relationship between the domain and range of R and R^-1. 

Problem 9 : 

If R is a relation on set A = {1, 2, 3, 4, 5, 6, 7, 8} given by xRy <=> y = 3x, then R = ?

(a) {(3, 1), (6, 2), (8, 2), (9, 3)}

(b) {(3, 1), (6, 2), (9, 3)}

(c) {(3, 1), (2, 6), (3, 9)}

(d) None of these

Problem 10 : 

Let A = {1, 2, 3}, B = {4, 6, 9} if relation R from A to B defined by x is greater then y. the range of R is -

(a) {1, 4, 6, 9}      (b) {4, 6, 9}      (c) {1}     (d) None of these.

Problem 11 :

Let ƒ : R → R be given by ƒ(x) = x²+3 Find

(i) {x : ƒ(x) = 28}

(ii) The pre-image of 39.

Detailed Answer Key

1. Answer : 

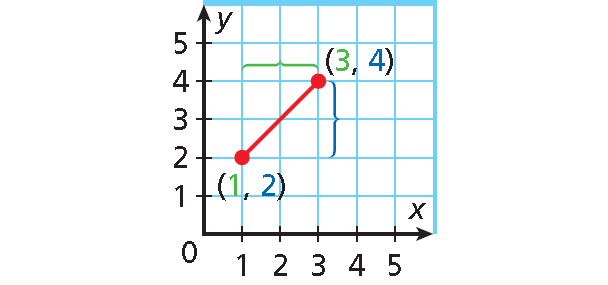
The domain is all x-values from 1 through 3, inclusive.

Domain : 1 ≤ x ≤ 3

The range is all y-values from 2 through 4, inclusive.

Range : 2 ≤ y ≤ 4

2. Answer : 

Domain  =  {1, 2, 5, 6}

Range  =  {-4, -1, 0}

3. Answer : 

Domain  =  {7, 9, 12, 15}

Range  =  {-7, -1, 0}

4. Answer : 

Domain  =  {1, 4, 8}

Range  =  {1, 4}

5. Answer :

R maps the elements from A to B using the rule

f(x)  =  x²

Then, we have

f(1)  =  1²  =  1

f(2)  =  2²  =  4

f(3)  =  3²  =  9

f(4)  =  4²  =  16

So, 

R  =  {(1, 1), (2, 4), (3, 9), (4, 16)}

Therefore, 

Domain (R)  =  {1, 2, 3, 4}

Range (R)  =  {1, 4, 9, 16}

6. Answer : 

From the arrow diagram shown above, 

R  =  {(1, 5), (2, 8), (3, 6)}

Therefore, 

Domain (R)  =  {1, 2, 3}

Range (R)  =  {5, 6, 8}

7. Answer : 

From the arrow diagram shown above, 

R  =  {(a, e), (c, e), (d, f)}

Therefore, 

Domain (R)  =  {a, c, d}

Range (R)  =  {d, e}

8. Answer : 

R  =  {(1, 1), (2, 3), (3, 4), (2, 7)}

Domain and range of R : 

Domain (R)  =  {1, 2, 3}

Range (R)  =  {1, 3, 4, 7}

Find inverse relation R^-1 :

R^-1  =  {(1, 1), (3, 2), (4, 3), (7, 2)}

Domain and range of R^-1 : 

Domain (R^-1)  =  {1, 3, 4, 7}

Range (R^-1)  =  {1, 2, 3}

Clearly,

Domain (R^-1)  =  Range (R)

Range (R^-1)  =  Domain (R)

9. Answer :

Domain of the function is A = {1, 2, 3, 4, 5, 6, 7, 8}

y = 3x

• If x = 1, y = 3(1) ==> 3
• If x = 2, y = 3(2) ==> 6
• If x = 3, y = 3(3) ==> 9
• If x = 4, y = 3(4) ==> 12
• If x = 5, y = 3(5) ==> 15
• If x = 6, y = 3(6) ==> 18
• If x = 7, y = 3(7) ==> 21
• If x = 8, y = 3(8) ==> 24

The required relation would be,

{(1, 3) (2, 6) (3, 9) (4, 12) (5, 15) (6, 18) (7, 21) (8, 24)} 

So, none of these is the answer.

10. Answer :

Here R is the relation from A to B, x > y

R = {(2, 1) (3, 1)}

So, the range = {1}. Option c is correct.

11. Answer :

Let ƒ : R → R be given by ƒ(x) = x²+3 Find

(i) {x : ƒ(x) = 28}

28 = x²+3

Subtracting 3, we get

x² = 28 - 3

x² = 25

x = -5 and 5.

(ii) The pre-images of 39.

Preimage of 39, when f(x) = 39

39 = x²+3

x² = 39 - 3

x² = 36

x = -6 and 6.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.