ENDPOINTS OF DIAMETER OF A CIRCLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In geometry, the endpoints of a diameter are the two points on the circumference of a circle that define the diameter. Diameter is a line segment passes through the center and it connects two points on the circle. The term "endpoints" refers to the two points at the extremes of this line segment.
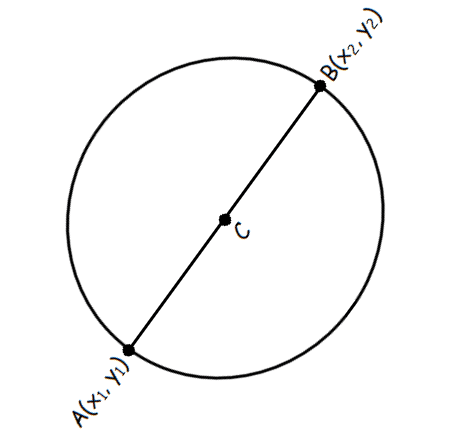
In the circle above, C is the center and AB is a diameter. A(x1, y1) and B(x2, y2) are the two end points of the diameter AB.
Note :
(i) The distance between the two endpoints of diameter is the length of the diameter.
(ii) One-half of the length of the diameter is equal to radius of the circle.
(iii) The midpoint of the two endpoints of diameter is the center of the circle.
(iv) The distance between one end point of diameter and center is equal to radius.
Solved Problems
Problem 1 :
If the two endpoints of diameter are (2, 3) and (-1, 5), find the center of the circle.
Solution :
Center of the circle is the midpoint of the two end points of diameter.
Midpoint of the line segment joining (x1, y1) and (x2, y2).
Substitute (x1, y1) = (2, 3) and (x2, y2) = (-1, 5).
= (½, 4)
Therefore, the center of the circle is (½, 4).
Problem 2 :
If the two endpoints of diameter are (, 4) and (-1, -2), find the length of the diameter.
Solution :
Lenth of diameter in a circle is the distance between the two endpoints of the diameter.
Distance between the two points (x1, y1) and (x2, y2) :
Substitute (x1, y1) = (8, 7) and (x2, y2) = (2, 10).
= 3√5
Therefore, the length of the diameter is 3√5 units.
Problem 3 :
If the two endpoints of diameter are (7, 4) and (-1, -2), find the radius of the circle.
Solution :
Distance between the two points (x1, y1) and (x2, y2) :
Substitute (x1, y1) = (7, 4) and (x2, y2) = (-1, -2) to find the length of diameter.
= √100
= 10 units
= ¹⁰⁄₂
= 5 units
Problem 4 :
The center of a circle is (-2, 3). If one end endpoint of diameter is (3, -5), find the other end point.
Solution :
We already know that the midpoint of two end points of diameter is equal to center of the circle.
Let (x1, y1) and (x2, y2) be the two end points of the diameter. Then, we have
One endpoint of the diameter is (-2, 3). Let (a, b) be the pother end point of the diameter.
Substitute (x1, y1) = (-2, 3) and (x2, y2) = (a, b).
Equate the x-coordinates and y-coordinates.
|
-2 + a = -4 a = -2 |
3 + b = 6 b = 3 |
(a, b) = (-2, 3)
The other end point of the diameter is (-2, 3).
Problem 5 :
If the two endpoints of diameter of a circle are (2, 3) and (6, -5), find the equation of the cricle in standard form.
Solution :
Center of the circle :
= midpoint of the end points of diameter
= (4, -1)
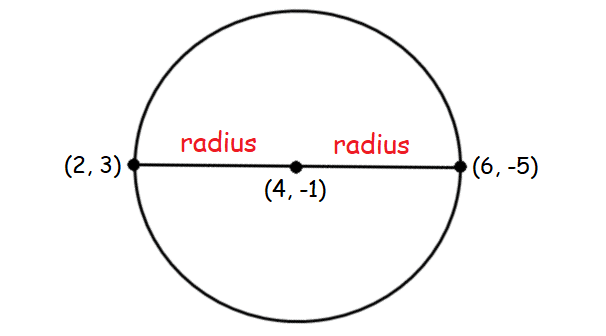
Distance between one end point of diameter (2, 3) and center of the circle (4, 1).
Radius = √8 units
Equation of a circle in standard form :
(x - h)2 + (y - k)2 = r2
where, center = (h, k) and radius = r.
Substitute (h, k) = (4, 1) and r = √8.
(x - 4)2 + (y - 1)2 = (√8)2
(x - 4)2 + (y - 1)2 = 8
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Times Table Shortcuts
Dec 30, 25 07:14 PM
Times Table Shortcuts - Concept - Examples -
10 Hard SAT Math Questions (Part - 42)
Dec 30, 25 05:52 AM
10 Hard SAT Math Questions (Part - 42) -
10 Hard SAT Math Questions (Part - 38)
Dec 29, 25 04:21 AM
10 Hard SAT Math Questions (Part - 38)

