EQUATION OF PARABOLA GIVEN FOCUS AND DIRECTRIX

In this section, you will learn how to find equation of the parabola, if its focus and directrix are given.

We can use the following formulas to find the distance between fixed point (F) and moving point(P) and the perpendicular distance between the moving point (P) and directrix (a fixed line).   

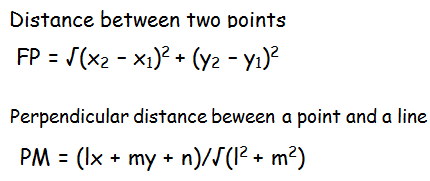
Example 1 :

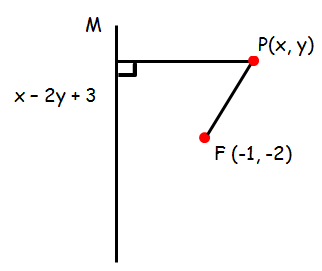
Find the equation of the parabola whose focus and directrix is (-1, -2) and x - 2y + 3 = 0

Solution :

Let P (x, y) be any point on the parabola. If PM is drawn perpendicular to the directrix respectively.

FP/PM = e

Since it is parabola e = 1

FP = PM

√(x + 1)² + (y + 2)² = (x-2y+3)/(√1²+2²)

√(x +1)² + (y+ 2)² = (x-2y+3)/(√5)

taking squares on both sides

(x+1)² + (y+2)² = (x-2y+3)²/5

5[x²+2x+1+y²+4y+4] = x²+4y²+9-4xy-12y+6x

5x²- x² + 4xy + 5y²- 4y²+ 10x - 6x + 20y + 12y + 25-9 = 0

4x²+ 4xy + y²+ 4x + 32y + 16 = 0

Example 2 :

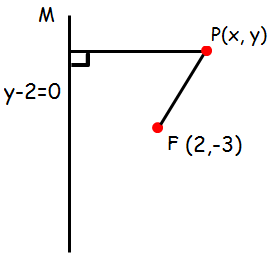
Find the equation of the parabola whose focus and directrix is (2, -3) and y - 2 = 0 respectively

Solution :

Let P (x, y) be any point on the parabola. If PM is drawn perpendicular to the directrix.

FP/PM = e

Since it is parabola e = 1

FP = PM

√(x-2)² + (y+3)² = (y-2)/(√0²+1²)

√(x-2)² + (y+3)² = (y-2)/√1

taking squares on both sides

(x-2)² + (y+3)² = (y-2)²

x² - 4 x + 4 + y² + 6 y + 9 = y² - 4y + 4

x² + y² - y²- 4 x + 6 y + 4 y + 9 + 4 - 4 = 0

x² - 4 x + 10 y + 9  = 0

Example 3 :

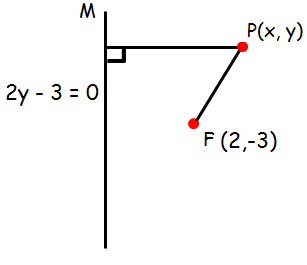
Find the equation of the parabola whose focus and directrix is (2, -3) and 2y - 3 = 0 respectively

Solution :

Let P (x, y) be any point on the parabola. If PM is drawn perpendicular to the directrix.

FP/PM = e

Since it is parabola e = 1

FP = PM

√(x-2)² + (y+3)² = (2y-3)/(√0²+2²)

√(x-2)² + (y+3)² = (2y-3)/√4

taking squares on both sides

(x-2)² + (y+3)² = (2y-3)²/4

4[x² - 4 x + 4 + y² + 6 y + 9] = 4y² - 12y + 9

4x² + 4y² - 4y² - 16x + 24y + 12y + 52 - 9 = 0

4x² - 16x + 36y + 43 = 0

Example 4 :

Find the equation of the parabola whose focus and directrix is (-1, 3) and 2x + 3y = 3 respectively

Solution :

Let P (x, y) be any point on the parabola. If PM is drawn perpendicular to the directrix.

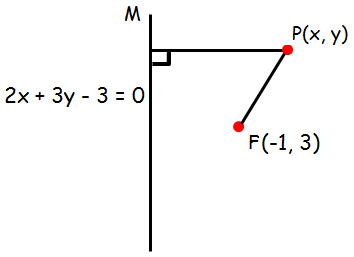
FP/PM = e

Since it is parabola e = 1

FP = PM

√(x+1)² + (y-3)² = (2x+3y-3)/(√2²+3²)

√(x+1)² + (y-3)² = (2x+3y-3)/√13

taking squares on both sides

(x+1)² + (y-3)² = (2x+3y-3)²/13

13[x²+2x+1+y²-6y+9] =  4x²+9y²+9+12xy-18y-12x

13x²-4x²-12xy+13y²-9y²+26x+12x-78y+18y+130-9 = 0

9 x²-12 x y + 4 y²+ 38 x - 60 y + 121 = 0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.