EQUATIONS OF STRAIGHT LINES WORKSHEET
Problem 1 :
Find the general form of equation of a straight line whose slope is 3 and y-intercept -2.
Problem 2 :
Find the general form of equation of a straight line passing through the points (-1, 1) and (2, -4).
Problem 3 :
Find the general equation of the straight line passing through the point (-2, 3) with slope 1/3.
Problem 4 :
Find the general equation of the straight line whose x-intercept -2 and y-intercept is 3.
Problem 5 :
Find the equation of a straight line parallel to y-axis and passing through (-5, 0).
Problem 6 :
Find the equation of a straight line parallel to x-axis and passing through (0, 6).
Problem 7 :
Find the equation of a straight shown below in slope-intercept form.
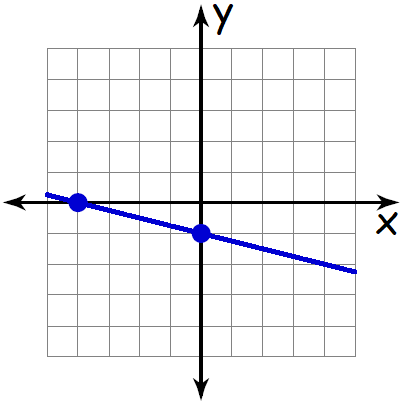
Problem 8 :
Find the equation of a straight shown below in slope-intercept form.
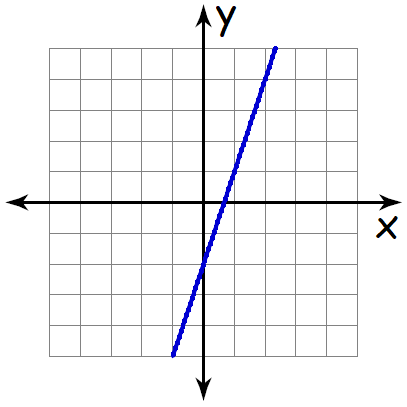

Answers
1. Answer :
Given : Slope m = 3 and y-intercept b = -2.
Equation of the straight line in slope-intercept form :
y = mx + b
Substitute m = 3 for m and b = -2.
y = 3x - 2
Subtract y from each side.
0 = 3x - y - 2
or
3x - y - 2 = 0
2. Answer :
Given : Two points on the straight line : (-1, 1) and (2, -4).
Equation of the straight line in two-points form is
(y - y1) / (y2 - y1) = (x - x1) / (x2 - x1)
Substitute (x1 , y1) = (-1, 1) and (x2, y2) = (2, -4).
(y - 1) / (-4 - 1) = (x + 1) / (2 + 1)
Simplify.
(y - 1) / (-5) = (x + 1) / 3
Cross multiply.
3(y - 1) = -5(x + 1)
3y - 3 = -5x - 5
5x + 3y + 2 = 0
3. Answer :
Given : Point = (-2, 3) and slope m = 1/3
Equation of the straight line in point-slope form is
y - y1 = m(x - x1)
Substitute (x1 , y1) = (-2 , 3) and m = 1/3.
y - 3 = 1/3 ⋅ (x + 2)
Multiply each side by 3.
3(y - 3) = x + 2
Simplify.
3y - 9 = x + 2
Subtract 3y from each side.
-9 = x - 3y + 2
Add 9 to each side.
0 = x - 3y + 11
or
x - 3y + 11 = 0
4. Answer :
Given : x-intercept is -2 and y-intercept is 3.
Equation of the straight line in intercept-form is
x/a + y/b = 1
Substitute a = -2 and b = 3.
x/(-2) + y/3 = 1 -----(1)
The lest common multiple of (2, 3) is 6.
So, multiply each side (1) by 6.
-3x + 2y = 6
Multiply each side by -1.
3x - 2y = -6
Add 6 to each side.
3x - 2y + 6 = 0
5. Answer :
Equation of a straight parallel to y-axis is
x = c
It is passing through the point (-5, 0)
Then,
-5 = c
So, the equation of the given line is
x = -5
or
x + 5 = 0
6. Answer :
Equation of a straight parallel to x-axis is
y = k
It is passing through the point (0, 6)
Then,
6 = k
So, the equation of the given line is
y = 6
or
x + 5 = 0
7. Answer :

The above line is a falling line. So, its slope will be a negative value.
Measure the rise and run.
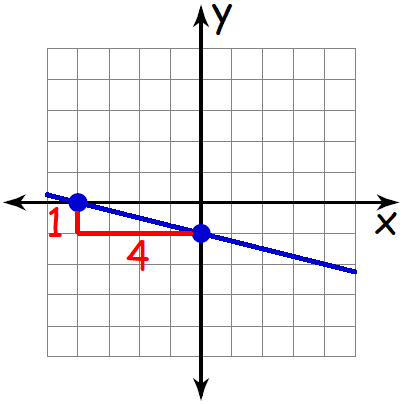
For the above line,
Rise = 1
Run = 4
Then,
Slope = rise / run
Slope = -1/4
From the graph shown above y-intercept is -1.
Equation of a straight line in slope-intercept form is
y = mx + b
Substitute m = -1/4 and b = -1.
y = (-1/4)x - 1
y = -x/4 - 1
8. Answer :

The above line is a falling line. So, its slope will be a positive value.
Measure the rise and run.
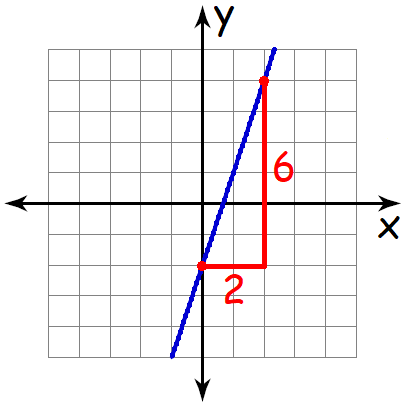
For the above line,
Rise = 6
Run = 2
Then,
Slope = rise / run
Slope = 6/2
Slope = 3
From the graph shown above y-intercept is -2.
Equation of a straight line in slope-intercept form is
y = mx + b
Substitute m = 3 and b = -2.
y = 3x - 2
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Resources (Videos, Concepts, Worksheets and More)
Dec 23, 24 03:47 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 91)
Dec 23, 24 03:40 AM
Digital SAT Math Problems and Solutions (Part - 91) -
Digital SAT Math Problems and Solutions (Part - 90)
Dec 21, 24 02:19 AM
Digital SAT Math Problems and Solutions (Part - 90)