EQUIVALENT FRACTIONS

The fractions which are equivalent have the same value, even though they may look different. These fractions are really the same.

For example, 

¾ = ⁶⁄₈ = ⁹⁄₁₆

Why are they the same ? 

Because, when we multiply or divide both the numerator and denominator by the same number, the fraction keeps it's value.

Understanding Equivalent Fractions

Let us divide a rectangle into two equal parts and shade one of the parts. 

In the above rectangle, the shaded part is ½. 

That is, in total of 2 parts, one part is shaded. 

Let us divide the same rectangle into four equal parts and shade 2 parts. 

In the above rectangle, the shaded part is ²⁄₄. 

That is, in total of 4 parts, two parts are shaded. 

Let us divide the same rectangle into six equal parts and shade 3 parts. 

In the above rectangle, the shaded part is ³⁄₆. 

That is, in total of 6 parts, three parts are shaded. 

In all the above figures, the shaded portion are equal but they can be represented by different fractions. 

½ = ²⁄₄ = ³⁄₆

When two or more fractions represent the same part of a whole, the fractions are called equivalent. 

Rule to Find Equivalent Fractions

Change both numerator and denominator using multiplication or division by the same number.

Example :

Using multiplication :  

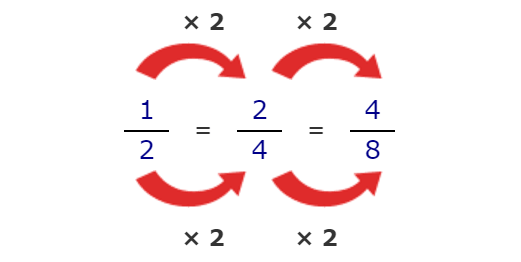
½, ²⁄₄ and ⁴⁄₈ are equivalent fractions.

Using division :

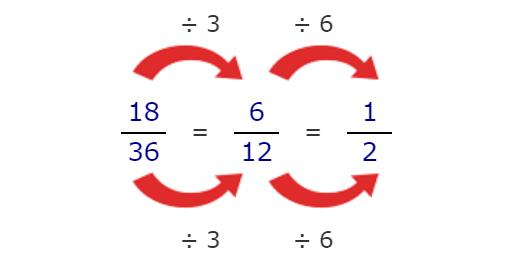
¹⁸⁄₃₆, ⁶⁄₁₂ and ½ are equivalent fractions.

Solved Problems 

Problem 1 :

Write 4 fractions which are equivalent to ⅚. 

Solution :

To find 4 fractions which are equivalent to ⅚, multiply both numerator and denominator of the fraction  ⅚ by 2, 3, 4 and 5.  

⅚ = ⁽⁵ˣ²⁾⁄₍₆ₓ₂₎ = ¹⁰⁄₁₂

⅚ = ⁽⁵ˣ³⁾⁄₍₆ₓ₃₎ = ¹⁵⁄₁₈

⅚ = ⁽⁵ˣ⁴⁾⁄₍₆ₓ₄₎ = ²⁰⁄₂₄

⅚ = ⁽⁵ˣ⁵⁾⁄₍₆ₓ₅₎ = ²⁵⁄₃₀

The four fractions which are equivalent to ⅚ are

¹⁰⁄₁₂, ¹⁵⁄₁₈, ²⁰⁄₂₄ and ²⁵⁄₃₀

Problem 2 :

Write 3 fractions which are equivalent to ³⁄₇. 

Solution :

³⁄₇ = ⁽³ˣ²⁾⁄₍₇ₓ₂₎ = ⁶⁄₁₄

³⁄₇ = ⁽³ˣ³⁾⁄₍₇ₓ₃₎ = ⁹⁄₂₁

³⁄₇ = ⁽³ˣ⁴⁾⁄₍₇ₓ₄₎ = ¹²⁄₂₈

The four fractions which are equivalent to ³⁄₇ are

⁶⁄₁₄, ⁹⁄₂₁ and ¹²⁄₂₈

Problem 3 :

Write 4 fractions which are equivalent to 0.03.

Solution :

Write 0.03 as as a fraction.

0.03 = ³⁄₁₀₀

To find 4 fractions which are equivalent to ³⁄₁₀₀, multiply both numerator and denominator of the fraction  ³⁄₁₀₀ by 2, 3, 4 and 5.

³⁄₁₀₀ = ⁽³ˣ²⁾⁄₍₁₀₀ₓ₂₎ = ⁶⁄₂₀₀

³⁄₁₀₀ = ⁽³ˣ³⁾⁄₍₁₀₀ₓ₃₎ = ⁹⁄₃₀₀

³⁄₁₀₀ = ⁽³ˣ⁴⁾⁄₍₁₀₀ₓ₄₎ = ¹²⁄₄₀₀

³⁄₁₀₀ = ⁽³ˣ⁵⁾⁄₍₁₀₀ₓ₅₎ = ¹⁵⁄₅₀₀

The four fractions which are equivalent to ³⁄₇ are

⁶⁄₂₀₀, ⁹⁄₃₀₀, ¹²⁄₄₀₀ and ¹⁵⁄₅₀₀

Problem 4 :

Pick out the fractions which are equivalent :

⅖, ¹²⁄₁₆, ⅓, ⁵⁄₁₅, ¹⁶⁄₄₀, ¾, ⁹⁄₁₂

Solution :

The fractions ⅖ and ¹⁶⁄₄₀ are equivalent.

Because,

⅖ = ⁽²ˣ⁸⁾⁄₍₅ₓ₈₎ = ¹⁶⁄₄₀

The fractions ¹²⁄₁₆, ¾ and ⁹⁄₁₂ are equivalent.

Because,

¹²⁄₁₆ = ⁽¹²^÷⁴⁾⁄₍₁₆_÷₄₎ = ¾

and

⁹⁄₁₂ = ⁽⁹^÷³⁾⁄₍₁₂_÷₃₎ = ¾

The fractions ⅓ and ⁵⁄₁₅ are equivalent.

Because,

⅓ = ⁽¹ˣ⁵⁾⁄₍₃ₓ₅₎ = ⁵⁄₁₅

Problem 5 :

Find the missing numbers :

⁵⁄₉ = ³⁵⁄? = ?⁄₇₂

Solution :

The numerator of the first two fractions are 5 and 35. And 5 will become 35, when we multiply 5 by 7. 

So, we have to multiply the denominator of the first fraction 9 by 7 in order to get the denominator of the second fraction.

9x7 = 63

Hence, the denominator of the second fraction is 63.

The denominator of the first and third fraction are 9 and 72. And 9 will become 72, when we multiply by 8. 

So, we have to multiply the numerator of the first fraction 5 by 8 in order to get the numerator of the third fraction. 

Hence, the numerator of the third fraction is 40.

⁵⁄₉ = ³⁵⁄₆₃ = ⁴⁰⁄₇₂

Problem 6 :

Find the missing numbers :

⅗ = ²¹⁄? = ?⁄₂₀

Solution :

The numerator of the first two fractions are 3 and 21. And 3 will become 21, when we multiply by 7. 

So, we have to multiply the denominator of the first fraction 5 by 7 in order to get the denominator of the second fraction. 

Hence, the denominator of the second fraction is 35.

The denominator of the first and third fraction are 5 and 20. And 5 will become 20, when we multiply by 4. 

So, we have to multiply the numerator of the first fraction 3 by 4 in order to get the numerator of the third fraction. 

Hence, the numerator of the third fraction is 12.

⅗ = ²¹⁄₃₅ = ¹²⁄₂₀

Problem 7 : 

If the following two fractions are equivalent, find the value of x.

⁹⁄₈ and ˣ⁄₅₆

Solution :

Since ⁹⁄₈ and ˣ⁄₅₆ are equivalent fractions,

⁹⁄₈ = ˣ⁄₅₆

The denominator on the right side is 56. In the fraction ⁹⁄₈, the denominator is 8. To get an equivalent fraction with denominator 56, we have to multiply both numerator and denominator of the fraction ⁹⁄₈ by 7.

⁽⁹ˣ⁷⁾⁄₍₈ₓ₇₎ = ˣ⁄₃₆

⁶³⁄₅₆ = ˣ⁄₃₆

The above two fractions are equivalent with the same denominator. Then, the numerators must be equal.

Therefore,

x = 63

Problem 8 : 

If the following two fractions are equivalent, find the value of y.

⁻⁶⁄₁₈ and ʸ⁄₃

Solution :

Since ⁻⁶⁄₁₈ and ʸ⁄₃ are equivalent fractions,

⁻⁶⁄₁₈ = ʸ⁄₃

The denominator on the left side is 3. In the fraction ⁻⁶⁄₁₈, the denominator is 18. To get an equivalent fraction with denominator 3, we have to divide both numerator and denominator of the fraction ⁻⁶⁄₁₈ by 6.

⁻⁽⁶^÷⁶⁾⁄₍₁₈_÷₆₎ = ʸ⁄₃

⁻¹⁄₃ = ʸ⁄₃

The above two fractions are equivalent with the same denominator. Then, the numerators must be equal.

Therefore,

y = -1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.