EXACT VALUES OF TRIGONOMETRIC FUNCTIONS OF WIDELY USED ANGLES

Let us list out the values of trigonometric functions at known angles.

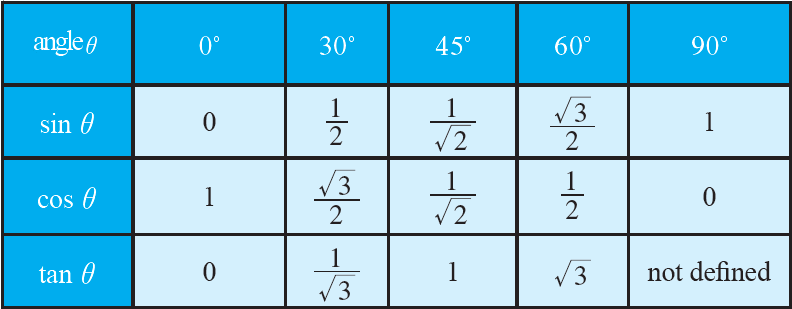
(i) The values given above are all exact.

(ii) We observe that sin 30° and cos 60° are equal. Also sin 60° and cos 30° are equal.

(iii) The value of reciprocal ratios namely cosecant, secant and cotangent can be obtained using the above table.

(iv) The result cos 90° = 0 does not allow us to define tan 90° and sec 90°.

(v) Similarly sin 0° = 0 does not permit us to define csc 0° and cot 0°.

Practice Problems

Problem 1 : 

Find the value of csc 30°. 

Solution : 

We know that sin θ and csc θ are reciprocal to each other. 

Then, 

csc 30°  =  1 / sin 30°

In the table above, sin 30°  =  1/2. 

Therefore,

csc 30°  =  1 / (1/2)

csc 30°  =  1 ⋅ (2/1)

csc 30°  =  (1 ⋅ 2) / 1

csc 30°  =  2/1

csc 30°  =  2

Problem 2 : 

Find the value of sec 45°. 

Solution : 

We know that cos θ and sec θ are reciprocal to each other. 

Then, 

sec 45°  =  1 / cos 45°

In the table above, cos 45°  =  1/√2. 

Therefore,

sec 45°  =  1 / (1/√2)

sec 45°  =  1 ⋅ (√2/1)

sec 45°  =  (1 ⋅ √2) / 1

sec 45°  =  √2/1

sec 45°  =  √2

Problem 3 : 

Find the value of cot 60°. 

Solution : 

We know that tan θ and cot θ are reciprocal to each other. 

Then, 

cot 60°  =  1 / tan 60°

In the table above, tan 60°  =  √3. 

Therefore,

cot 60°  =  1 / √3

Problem 4 : 

Find the value of sec 90°. 

Solution : 

We know that cos θ and sec θ are reciprocal to each other. 

Then, 

sec 90°  =  1 / cos 90°

In the table above, cos 90°  =  0. 

Therefore,

sec 90°  =  1 / 0

sec 90°  =  not defined

Problem 5 : 

Find the value of sin²45° + cos²45°. 

Solution : 

In the table above, sin 45°  =  1/√2 and cos 45°  =  1/√2.

Then, 

sin²45° + cos²45°  =  (sin 45°)² + (cos 45°)²

sin²45° + cos²45°  =  (1/√2)² + (1/√2)²

sin²45° + cos²45°  =  1/2 + 1/2

sin²45° + cos²45°  =  (1 + 1) / 2

sin²45° + cos²45°  =  2/2

sin²45° + cos²45°  =  1

Problem 6 : 

Find the value of sin 30° ⋅ csc 30° + tan 30° ⋅ cot 60°.  

Solution : 

In the table above,

sin 30°  =  1/2

csc 30°  =  1 / sin 30°  =  2

tan 30°  =  1/√3

cot 60°  =  1 / tan 60°  =  1/√3

Then, the value of (sin 30° ⋅ csc 30° + tan 30° ⋅ cot 60°) is 

=  (1/2) ⋅ (2)  +  (1/√3) ⋅ (1/√3)

=  1 + 1/3

=  3/3 + 1/3

=  (3 + 1) / 3

=  4/3  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.